Lysario – by Panagiotis Chatzichrisafis
"ούτω γάρ ειδέναι το σύνθετον υπολαμβάνομεν, όταν ειδώμεν εκ τίνων και πόσων εστίν …"
Archive for the ‘Kay: Modern Spectral Estimation, Theory and Application’ Category
Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”,p. 60 exercise 3.1
Author: Panagiotis10 Okt
In [1, p. 60 exercise 3.1] a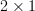 
real random vector 
is given , which is distributed according to a multivatiate Gaussian PDF with zero mean and covariance matrix:
We are asked to find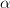
if 
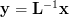where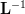 
is given by the relation:
so that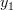
and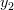 
are uncorrelated and hence independent. We are also asked to find the Cholesky decomposition of
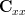which expresse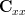s as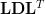 
, where 
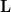is lower triangular with 1′s on the principal diagonal and 
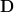is a diagonal matrix with positive diagonal elements. read the conclusion >
real random vector is given , which is distributed according to a multivatiate Gaussian PDF with zero mean and covariance matrix:
![\mathbf{C}_{xx}=
\left[
\begin{array}{cc}
\sigma_{1}^2 & \sigma_{12} \\
\sigma_{21} & \sigma_{2}^2
\end{array}\right]](https://lysario.de/wp-content/cache/tex_372170732f621d352bb5f0949e11915d.png) | |||
We are asked to find
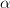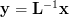if where 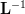is given by the relation: |  |  | |
| |  |
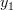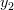so that
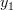and 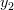are uncorrelated and hence independent. We are also asked to find the Cholesky decomposition of
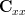which expresse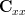s as 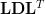, where 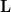is lower triangular with 1′s on the principal diagonal and 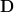is a diagonal matrix with positive diagonal elements. read the conclusion >
Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”,p. 35 exercise 2.18
Author: Panagiotis22 Aug
In [1, p. 35 exercise 2.18] we are asked to prove that the inverse of a complex matrix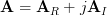 
may be found by first inverting
to yield
and then letting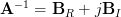
.
read the conclusion >
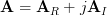may be found by first inverting
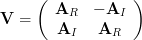 | (1) | ||
to yield
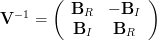 | (2) | ||
and then letting
.
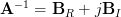read the conclusion >
Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”,p. 35 exercise 2.17
Author: Panagiotis16 Aug
In [1, p. 35 exercise 2.17] we are asked to verify the alternative expression [1, p. 33 (2.77)] for a hermitian function.
read the conclusion >
Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”,p. 35 exercise 2.16
Author: Panagiotis12 Aug
In [1, p. 35 exercise 2.16] we are asked to verify the formulas given for the complex gradient of a hermitian and a linear form [1, p. 31 (2.70)]. To do so, we are instructed to decompose the matrices and vectors into their real and imaginary parts as
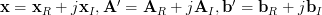read the conclusion >
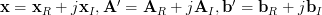read the conclusion >
Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”,p. 35 exercise 2.15
Author: Panagiotis25 Jun
In [1, p. 35 exercise 2.15] we are asked to verify the formulas given for the gradient of a quadratic and linear form [1, p. 31 (2.61)].
The corresponding formulas are
and
where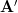
is a symmetric 
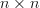matrix with elements 
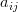and 
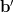is a real 
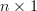vector with elements 
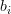and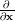 
denotes the gradient of a real function in respect to
.
read the conclusion >
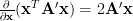 | (1) | ||
and
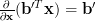 | (2) | ||
where
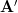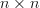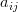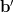is a symmetric matrix with elements and is a real 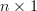vector with elements 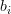and 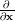denotes the gradient of a real function in respect to
.
read the conclusion >