Lysario – by Panagiotis Chatzichrisafis
"ούτω γάρ ειδέναι το σύνθετον υπολαμβάνομεν, όταν ειδώμεν εκ τίνων και πόσων εστίν …"
Archive for the ‘Quantum Mechanics’ Category
Liboff: “Introductory Quantum Mechanics”, 2nd edition p.86 exercise 3.16
Author: Panagiotis2 Jan
The exercise [1, p. 86 ex. 3.16] asks to prove that if the eigenfunctions and eigenvalues of an operator 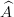 are
are 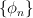 and
and 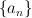 , respectively (
, respectively (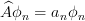 ) then the eigenfunctions of a function
) then the eigenfunctions of a function 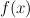 having an expansion of the form:
having an expansion of the form:
will also be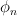 with corresponding eigenvalues
with corresponding eigenvalues 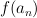 ,
, 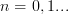 . That is
. That is 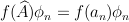 .
read the conclusion >
.
read the conclusion >
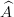 are
are 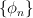 and
and 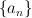 , respectively (
, respectively (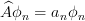 ) then the eigenfunctions of a function
) then the eigenfunctions of a function 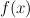 having an expansion of the form:
having an expansion of the form:
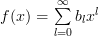 | (1) | ||
will also be
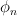 with corresponding eigenvalues
with corresponding eigenvalues 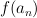 ,
, 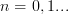 . That is
. That is 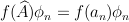 .
read the conclusion >
.
read the conclusion >