Lysario – by Panagiotis Chatzichrisafis
"ούτω γάρ ειδέναι το σύνθετον υπολαμβάνομεν, όταν ειδώμεν εκ τίνων και πόσων εστίν …"
Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”,p. 60 exercise 3.3
Author: Panagiotis4 Dez
In [1, p. 60 exercise 3.3] we are asked to prove that the complex multivariate Gaussian PDF reduces to the complex univariate Gaussian PDF if N=1.
Solution: The complex multivariate Gaussian PDF is given by [1, p. 44, (3.13)] :
with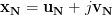 denoting an
denoting an  dimensional complex vector, which is composed of the real
dimensional complex vector, which is composed of the real  dimensional vectors
dimensional vectors
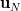 and
and 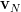 .
The univariate complex gaussian probability density function is given by [1, p. 44, (3.10)] :
.
The univariate complex gaussian probability density function is given by [1, p. 44, (3.10)] :
with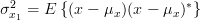 where
where 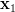 is a one dimensional complex variable with
is a one dimensional complex variable with 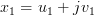 ,
, 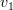 and
and 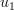 being real variables.
For
being real variables.
For 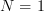 in (1) we obtain for the covariance matrix
in (1) we obtain for the covariance matrix 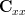 the following relation:
the following relation:
and thus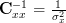 . The determinant of an single element matrix is per definition the element value itself ([2, p. 326]), thus
. The determinant of an single element matrix is per definition the element value itself ([2, p. 326]), thus
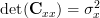 for
for 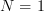 .
Replacing
.
Replacing 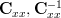 and
and 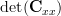 in (1) while setting
in (1) while setting 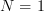 we obtain:
we obtain:
which is equal to (2). QED.
[1] Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”, Prentice Hall, ISBN: 0-13-598582-X.
[2] Lawrence J. Corwin and Robert H. Szczarba: “Calculus in Vector Spaces”, Marcel Dekker, Inc, 2nd edition, ISBN: 0824792793.
Solution: The complex multivariate Gaussian PDF is given by [1, p. 44, (3.13)] :
![p(\mathbf{x_{N}})=\frac{1}{\pi^{N}det(\mathbf{C}_{xx})}exp\left[-(\mathbf{x_{N}}-\mathbf{\mu}_{\mathbf{x}_{N}})^{H}\mathbf{C}^{-1}_{xx}(\mathbf{x_{N}}-\mathbf{\mu}_{\mathbf{x}_{N}})\right]](https://lysario.de/wp-content/cache/tex_503bdcfc51b8526bd0ba8e99932c181c.png) | (1) | ||
with
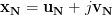 denoting an
denoting an  dimensional complex vector, which is composed of the real
dimensional complex vector, which is composed of the real  dimensional vectors
dimensional vectors
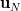 and
and 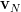 .
The univariate complex gaussian probability density function is given by [1, p. 44, (3.10)] :
.
The univariate complex gaussian probability density function is given by [1, p. 44, (3.10)] :
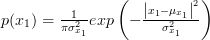 | (2) | ||
with
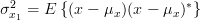 where
where 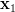 is a one dimensional complex variable with
is a one dimensional complex variable with 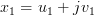 ,
, 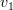 and
and 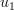 being real variables.
For
being real variables.
For 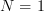 in (1) we obtain for the covariance matrix
in (1) we obtain for the covariance matrix 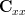 the following relation:
the following relation:
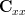 |  | 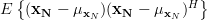 | |
 | 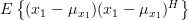 | ||
 | 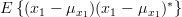 | ||
 |  |
and thus
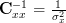 . The determinant of an single element matrix is per definition the element value itself ([2, p. 326]), thus
. The determinant of an single element matrix is per definition the element value itself ([2, p. 326]), thus
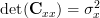 for
for  .
Replacing
.
Replacing 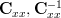 and
and 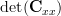 in (1) while setting
in (1) while setting 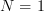 we obtain:
we obtain:
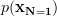 |  | ![\frac{1}{\pi \sigma_{x}^{2}}exp\left[ -\frac{(x_{1}-\mu_{x_{1}})^{H}( x_{1}-\mu_{x_{1}})}{\sigma_{x}^{2}}\right]](https://lysario.de/wp-content/cache/tex_b7367f00ef576e538fac21211138283c.png) | |
 | ![\frac{1}{\pi \sigma_{x}^{2}}exp\left[-\frac{\left|x_{1} -\mathbf{\mu}_{x_{1} }\right|^{2}}{\sigma_{x_{1}}^{2}}\right]](https://lysario.de/wp-content/cache/tex_f15131b93c3f105d962b7dd1e43bafac.png) |
which is equal to (2). QED.
[1] Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”, Prentice Hall, ISBN: 0-13-598582-X.
[2] Lawrence J. Corwin and Robert H. Szczarba: “Calculus in Vector Spaces”, Marcel Dekker, Inc, 2nd edition, ISBN: 0824792793.
3 Responses for "Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”,p. 60 exercise 3.3"
hi dear Panagiotis Chatzichrisafis,
your solutions were really usefull. but i need some other solutions of this book( Modern Spectral Estimation ).
could you please help me?
the problems are:
4.1, 4.8, 5.1, 5.3, 5.9, 5.13, 6.1, 6.4, 6.5, 6.10, 6.11
Hi Forooz,
i am happy to hear that some of the solutions i post are helpfull.
I have currently reviewed solutions up to exercize 5.2 , but i haven’t transferred them into digital form. Please be patient, I’ll try to post asap some solutions of the problems
you asked for, but i can’t promise any dates. May i ask what your profession is ?
Kind regards
P. Chatzichrisafis
Hi- just wanted to thank you for these solutions, they were really helpful! Keep up the good work!
Leave a reply