Lysario – by Panagiotis Chatzichrisafis
"ούτω γάρ ειδέναι το σύνθετον υπολαμβάνομεν, όταν ειδώμεν εκ τίνων και πόσων εστίν …"
Archive for the ‘Solved Problems’ Category
Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”,p. 94 exercise 4.2
Author: Panagiotis24 Jun
In [1, p. 94 exercise 4.2] we are asked to consider the estimator
where
for the process of Problem 4.1. We are informed that this estimator may be viewed as an averaged periodogram. In this point of view the data record is sectioned into blocks (in this case, of length 1) and the periodograms for each block are averaged. We are asked to find the mean and variance of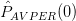
and compare the result to that obtained in [2].
read the conclusion >
 | (1) | ||
where
![\hat{P}_{PER}^{m}(0)= x^{2}[m]](https://lysario.de/wp-content/cache/tex_111f972a11d36418820c12baa2503f8a.png) | (2) | ||
for the process of Problem 4.1. We are informed that this estimator may be viewed as an averaged periodogram. In this point of view the data record is sectioned into blocks (in this case, of length 1) and the periodograms for each block are averaged. We are asked to find the mean and variance of
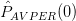and compare the result to that obtained in [2].
read the conclusion >
Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”,p. 94 exercise 4.1
Author: Panagiotis1 Feb
In problem [1, p. 94 exercise 4.1] we will show that the periodogram is an inconsistent estimator by examining the estimator at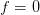 
, or
If![x[n]](https://lysario.de/wp-content/cache/tex_d3baaa3204e2a03ef9528a7d631a4806.png)
is real white Gaussian noise process with PSD
we are asked to find the mean an variance of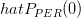
. We are asked if the variance converge to zero as 
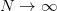. The hint provided within the exercise is to note that
where the quantiiy inside the parenthesis is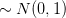
read the conclusion >
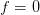, or
![\hat{P}_{PER}(0)=\frac{1}{N}\left(\sum\limits_{n=0}^{N-1}x[n]\right)^{2}.](https://lysario.de/wp-content/cache/tex_938765f09480f77020c3aad219444ca0.png) | (1) | ||
If
is real white Gaussian noise process with PSD
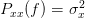 | (2) | ||
we are asked to find the mean an variance of
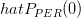. We are asked if the variance converge to zero as 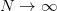. The hint provided within the exercise is to note that
![\hat{P}_{PER}(0)= \sigma_{x}^{2} \left(\sum\limits_{n=0}^{N-1}\frac{x[n]}{\sigma_{x}\sqrt{N}}\right)^{2}](https://lysario.de/wp-content/cache/tex_df83a5d6a6944d47bfd3d103cb81d6c4.png) | (3) | ||
where the quantiiy inside the parenthesis is
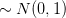read the conclusion >
Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”,p. 62 exercise 3.19
Author: Panagiotis17 Mai
In [1, p. 62 exercise 3.19] we are asked to find for the multiple sinusoidal process
the ensemble ACF and the temporal ACF as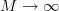
, where the 
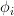‘s are all uniformly distributed random variables on 
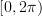and independent of each other. We are also asked to determine if this random process is autocorrelation ergodic.
read the conclusion >
![x[n]=\sum\limits_{i=1}^{P}A_{i}\cos(2\pi f_{i}n+\phi_{i})](https://lysario.de/wp-content/cache/tex_18c06f6747166204af88405a37dafba0.png) | |||
the ensemble ACF and the temporal ACF as
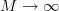, where the 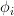‘s are all uniformly distributed random variables 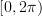on and independent of each other. We are also asked to determine if this random process is autocorrelation ergodic.
read the conclusion >
Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”,p. 62 exercise 3.18
Author: Panagiotis24 Aug
In [1, p. 62 exercise 3.18] we are asked to find the temporal autocorrelation function for the real sinusoidal random process of Problem [1, p. 62 exercise 3.16]:
as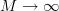
. As a second step we are asked to determine if the random process autocorrelation ergodic.
read the conclusion >
![\hat{r}_{xx}[k]=\frac{1}{2M+1}\sum\limits_{n=-M}^{M}x[n]x[n+k]](https://lysario.de/wp-content/cache/tex_e2a95ef4fe5209acc420201c8b3143bb.png) | |||
as
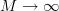. As a second step we are asked to determine if the random process autocorrelation ergodic.
read the conclusion >
Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”,p. 62 exercise 3.17
Author: Panagiotis19 Apr
In [1, p. 62 exercise 3.17] we are asked to verify that the variance of the sample mean estimator for the mean of a real WSS random process
is given by [1, eq. (3.60), p. 58]. For the case when is real white noise we are asked to what the variance expression does reduce to.
A hint that is given is to use the relationship from [1, eq. (3.64), p. 59].
read the conclusion >
![\frac{1}{2M+1}\sum\limits_{n=-M}^{n=M}x[n]](https://lysario.de/wp-content/cache/tex_1802f56fef4f03089a8b530f29ffae10.png) | |||
is given by [1, eq. (3.60), p. 58]. For the case when
is real white noise we are asked to what the variance expression does reduce to.
A hint that is given is to use the relationship from [1, eq. (3.64), p. 59].
read the conclusion >