Lysario – by Panagiotis Chatzichrisafis
"ούτω γάρ ειδέναι το σύνθετον υπολαμβάνομεν, όταν ειδώμεν εκ τίνων και πόσων εστίν …"
Archive for the ‘Kay: Modern Spectral Estimation, Theory and Application’ Category
Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”,p. 62 exercise 3.16
Author: Panagiotis13 Apr
In [1, p. 62 exercise 3.16] we are asked to show that the random process
, where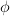
is uniformly distributed on 
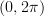, is WSS by finding its mean and ACF. Using the same assumptions we are asked to repeat the exercise for a single complex sinusoid
read the conclusion >
![x[n]= A \cos(2\pi f_{0}n+\phi)](https://lysario.de/wp-content/cache/tex_2601f4a14f4a21685c3519fd9aad5951.png) | (1) | ||
, where
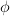is uniformly distributed on 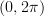, is WSS by finding its mean and ACF. Using the same assumptions we are asked to repeat the exercise for a single complex sinusoid
![x[n]=A\exp[j(2\pi f_{0}n+\phi)].](https://lysario.de/wp-content/cache/tex_b5f22b91c82ff2c5d69179471bd04442.png) | (2) | ||
read the conclusion >
Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”,p. 62 exercise 3.15
Author: Panagiotis24 Mrz
In [1, p. 62 exercise 3.15] it is requested to verify the ACF and PSD relationships given in [1, p. 53 eq. (3.50)] and [1, p. 54 eq. (3.51)].
read the conclusion >
Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”,p. 62 exercise 3.14
Author: Panagiotis4 Mrz
In [1, p. 62 exercise 3.14] it is requested to proof prove that the autocorrelation matrix given by [1, eq. 3.46] is also positive semidefinite. This shall be done by usage of the definition of the semidefinite property of the ACF in [1, eq. 3.45].
read the conclusion >
Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”,p. 62 exercise 3.13
Author: Panagiotis23 Feb
In [1, p. 62 exercise 3.13] it is requested to prove that the PSD of a real WSS random process is a real even function of frequency.
read the conclusion >
Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”,p. 62 exercise 3.12
Author: Panagiotis20 Feb
In [1, p. 62 exercise 3.12] we are asked to prove that for a WSS random process
read the conclusion >
![r_{xx}[-k]=r^{\ast}[k].](https://lysario.de/wp-content/cache/tex_071339ccd44d4617847bbb3e15dcf5ba.png) | (1) | ||
read the conclusion >