Lysario – by Panagiotis Chatzichrisafis
"ούτω γάρ ειδέναι το σύνθετον υπολαμβάνομεν, όταν ειδώμεν εκ τίνων και πόσων εστίν …"
Archive for the ‘Kay: Modern Spectral Estimation, Theory and Application’ Category
Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”,p. 34 exercise 2.9
Author: Panagiotis5 Jan
In [1, p. 34 exercise 2.9] we are asked to prove that the rank of the complex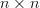 
matrix
where the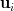
are linearly independent complex 
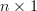vectors and the 
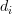‘s are real and positive, is equal to 
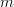if 
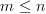. Furthermore we are asked what the rank equals to if 
> 
.
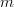read the conclusion >
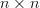matrix
 | (1) | ||
where the
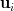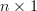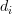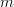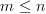are linearly independent complex vectors and the ‘s are real and positive, is equal to if . Furthermore we are asked what the rank equals to if > .
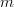read the conclusion >
Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”,p. 34 exercise 2.8
Author: Panagiotis22 Dez
In exercise [1, p. 34 exercise 2.8] we are asked to find the inverse of the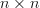 
hermitian matrix 
given by [1, (2.27)] by recursively applying Woodbury’s identity. This should be done by considering the cases where 
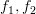are arbitrary and where 
, 
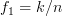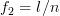for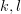 
beeing distinct integers in the range ![\left[ -n/2,n/2-1 \right]](https://lysario.de/wp-content/cache/tex_349760367e158b72823c089231e45245.png)
for even and ![\left[ -(n-1)/2,(n-1)/2 \right]](https://lysario.de/wp-content/cache/tex_bbbbf77ffaa65be463cde297b83e452b.png)
for odd.
read the conclusion >
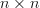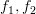hermitian matrix given by [1, (2.27)] by recursively applying Woodbury’s identity. This should be done by considering the cases where are arbitrary and where 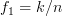, 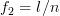for 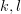beeing distinct integers in the range for even and for odd.
read the conclusion >
Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”,p. 34 exercise 2.7
Author: Panagiotis20 Nov
In exercise [1, p. 34 exercise 2.7] it is requested to find the inverse of the real symmetric Toeplitz matrix
and show that it is symmetric and persymmetric. read the conclusion >
![\mathbf{A} = \left[ {\begin{array}{*{20}c}
1 & { - a} & {a^2 } \\
{ - a} & 1 & { - a} \\
{a^2 } & { - a} & 1 \\
\end{array}} \right]](https://lysario.de/wp-content/cache/tex_7d981ef3134de2499a9848c900a503e7.png) | (1) | ||
and show that it is symmetric and persymmetric. read the conclusion >
Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”,p. 34 exercise 2.6
Author: Panagiotis16 Nov
In problem [1, p. 34 exercise 2.6] we are asked to prove that if 
and 
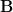are complex 
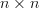Hermitian matrices and 
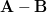is positive semidefinite, then ![\left[\mathbf{A}\right]_{ii} \geq \left[\mathbf{B}\right]_{ii}](https://lysario.de/wp-content/cache/tex_3652289cddad029917d54c1a0ed7c8cd.png)
.
read the conclusion >
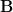and are complex 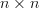Hermitian matrices and 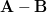is positive semidefinite, then .
read the conclusion >
Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”,p. 34 exercise 2.3
Author: Panagiotis27 Sep
In exercise [1, p. 34 exercise 2.3] we are asked to prove that the normalized DFT matrix given in [1, p. 21, (2.22)] is unitary.
read the conclusion >