Lysario – by Panagiotis Chatzichrisafis
"ούτω γάρ ειδέναι το σύνθετον υπολαμβάνομεν, όταν ειδώμεν εκ τίνων και πόσων εστίν …"
Archive for April, 2012
Book Review: Logicomix – An epic search for the truth
Author: Panagiotis26 Apr
Last year i got a very different mathematical book as a gift. A comic novel from Doxiadis, Papadimitriou and Papadatos: Logicomix. It is easy to read and provides some insight of the mathematical quest in the area of logic of the last century. You’ll meet people like Bertrand Russel, David Hilbert, Gödel and many more outstanding persons. Some work results of the main actors are presented in that way that is accessible for a wide audience – according to the rules used in popular science media. So even mathematical illiterate persons may enjoy the comic and due to the very nice illustrations i think even kids could enjoy it. The “showdown” is Gödel’s incompleteness theorem and i enjoyed the way the result was presented. The authors admit at the end of the book that the storyline is only loosely based on historical facts but actually this doesn’t reduce the value of the novel. Reading this comic was a nice way to relax during a cold winter’s day. Give it a try !
Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”,p. 62 exercise 3.17
Author: Panagiotis19 Apr
In [1, p. 62 exercise 3.17] we are asked to verify that the variance of the sample mean estimator for the mean of a real WSS random process
is given by [1, eq. (3.60), p. 58]. For the case when![x[n]](https://lysario.de/wp-content/cache/tex_d3baaa3204e2a03ef9528a7d631a4806.png) is real white noise we are asked to what the variance expression does reduce to.
A hint that is given is to use the relationship from [1, eq. (3.64), p. 59].
read the conclusion >
is real white noise we are asked to what the variance expression does reduce to.
A hint that is given is to use the relationship from [1, eq. (3.64), p. 59].
read the conclusion >
![\frac{1}{2M+1}\sum\limits_{n=-M}^{n=M}x[n]](https://lysario.de/wp-content/cache/tex_1802f56fef4f03089a8b530f29ffae10.png) | |||
is given by [1, eq. (3.60), p. 58]. For the case when
![x[n]](https://lysario.de/wp-content/cache/tex_d3baaa3204e2a03ef9528a7d631a4806.png) is real white noise we are asked to what the variance expression does reduce to.
A hint that is given is to use the relationship from [1, eq. (3.64), p. 59].
read the conclusion >
is real white noise we are asked to what the variance expression does reduce to.
A hint that is given is to use the relationship from [1, eq. (3.64), p. 59].
read the conclusion >
Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”,p. 62 exercise 3.16
Author: Panagiotis13 Apr
In [1, p. 62 exercise 3.16] we are asked to show that the random process
, where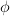 is uniformly distributed on
is uniformly distributed on 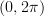 , is WSS by finding its mean and ACF. Using the same assumptions we are asked to repeat the exercise for a single complex sinusoid
, is WSS by finding its mean and ACF. Using the same assumptions we are asked to repeat the exercise for a single complex sinusoid
read the conclusion >
![x[n]= A \cos(2\pi f_{0}n+\phi)](https://lysario.de/wp-content/cache/tex_2601f4a14f4a21685c3519fd9aad5951.png) | (1) | ||
, where
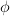 is uniformly distributed on
is uniformly distributed on 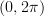 , is WSS by finding its mean and ACF. Using the same assumptions we are asked to repeat the exercise for a single complex sinusoid
, is WSS by finding its mean and ACF. Using the same assumptions we are asked to repeat the exercise for a single complex sinusoid
![x[n]=A\exp[j(2\pi f_{0}n+\phi)].](https://lysario.de/wp-content/cache/tex_b5f22b91c82ff2c5d69179471bd04442.png) | (2) | ||
read the conclusion >