Lysario – by Panagiotis Chatzichrisafis
"ούτω γάρ ειδέναι το σύνθετον υπολαμβάνομεν, όταν ειδώμεν εκ τίνων και πόσων εστίν …"
Export data from Scilab for PSTricks plots
Author: Panagiotis25 Jan
It is possible to load data from a file for plots with PSTricks in TeX. According to the PSTricks manual all that is needed is a file with a list of coordinate pairs delimited by curly braces , parentheses, commas. read the conclusion >
Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”,p. 94 exercise 4.2
Author: Panagiotis24 Jun
In [1, p. 94 exercise 4.2] we are asked to consider the estimator
where
for the process of Problem 4.1. We are informed that this estimator may be viewed as an averaged periodogram. In this point of view the data record is sectioned into blocks (in this case, of length 1) and the periodograms for each block are averaged. We are asked to find the mean and variance of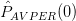
and compare the result to that obtained in [2].
read the conclusion >
 | (1) | ||
where
![\hat{P}_{PER}^{m}(0)= x^{2}[m]](https://lysario.de/wp-content/cache/tex_111f972a11d36418820c12baa2503f8a.png) | (2) | ||
for the process of Problem 4.1. We are informed that this estimator may be viewed as an averaged periodogram. In this point of view the data record is sectioned into blocks (in this case, of length 1) and the periodograms for each block are averaged. We are asked to find the mean and variance of
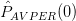and compare the result to that obtained in [2].
read the conclusion >
Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”,p. 94 exercise 4.1
Author: Panagiotis1 Feb
In problem [1, p. 94 exercise 4.1] we will show that the periodogram is an inconsistent estimator by examining the estimator at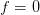 
, or
If![x[n]](https://lysario.de/wp-content/cache/tex_d3baaa3204e2a03ef9528a7d631a4806.png)
is real white Gaussian noise process with PSD
we are asked to find the mean an variance of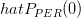
. We are asked if the variance converge to zero as 
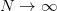. The hint provided within the exercise is to note that
where the quantiiy inside the parenthesis is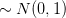
read the conclusion >
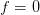, or
![\hat{P}_{PER}(0)=\frac{1}{N}\left(\sum\limits_{n=0}^{N-1}x[n]\right)^{2}.](https://lysario.de/wp-content/cache/tex_938765f09480f77020c3aad219444ca0.png) | (1) | ||
If
is real white Gaussian noise process with PSD
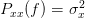 | (2) | ||
we are asked to find the mean an variance of
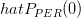. We are asked if the variance converge to zero as 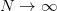. The hint provided within the exercise is to note that
![\hat{P}_{PER}(0)= \sigma_{x}^{2} \left(\sum\limits_{n=0}^{N-1}\frac{x[n]}{\sigma_{x}\sqrt{N}}\right)^{2}](https://lysario.de/wp-content/cache/tex_df83a5d6a6944d47bfd3d103cb81d6c4.png) | (3) | ||
where the quantiiy inside the parenthesis is
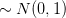read the conclusion >
Installing OpenCV 2.4.7 on MacOS Snow Leopard and get it work with macam drivers
Author: Panagiotis31 Jan
I recently wanted to update my OpenCV installation and try to find out why my usb camera – using the macam drivers – was not working with the libraries installed on my system. So this time i had the intention to dig into the code of OpenCV release. That meant using the easy way – mac ports – to install the OpenCV libraries was not an option.
read the conclusion >
Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”,p. 62 exercise 3.19
Author: Panagiotis17 Mai
In [1, p. 62 exercise 3.19] we are asked to find for the multiple sinusoidal process
the ensemble ACF and the temporal ACF as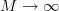
, where the 
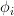‘s are all uniformly distributed random variables on 
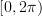and independent of each other. We are also asked to determine if this random process is autocorrelation ergodic.
read the conclusion >
![x[n]=\sum\limits_{i=1}^{P}A_{i}\cos(2\pi f_{i}n+\phi_{i})](https://lysario.de/wp-content/cache/tex_18c06f6747166204af88405a37dafba0.png) | |||
the ensemble ACF and the temporal ACF as
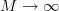, where the 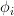‘s are all uniformly distributed random variables 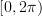on and independent of each other. We are also asked to determine if this random process is autocorrelation ergodic.
read the conclusion >