Lysario – by Panagiotis Chatzichrisafis
"ούτω γάρ ειδέναι το σύνθετον υπολαμβάνομεν, όταν ειδώμεν εκ τίνων και πόσων εστίν …"
Archive for April, 2010
Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”,p. 34 exercise 2.13
Author: Panagiotis27 Apr
In [1, p. 34 exercise 2.13] we are asked to consider the problem of fitting the data ![\left\{x[0],...,x[N-1]\right\}](https://lysario.de/wp-content/cache/tex_9ceb2dd63d7268e57f2b85d862426d56.png)
by the sum of a dc signal and a sinusoid as:
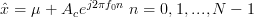. The complex dc level 
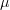and the sinusoidal amplitude 
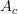are unknown and we are notified that we may view the determination of 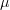, 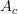as the solution of the overdetermined set of equations.
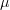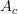It is asked to find the least squares solution for and . If furthermore 
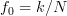, where 
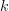is a nonzero integer in the range ![[-N/2,N/2-1]](https://lysario.de/wp-content/cache/tex_3a5bf53d3e9902f7fffe9d68b2de1428.png)
for 
even and ![[-(N-1)/2,(N-1)/2]](https://lysario.de/wp-content/cache/tex_dde8f99f860237fa0b573d2ad067620a.png)
for odd we are asked to determine again the least squares solution.
read the conclusion >
by the sum of a dc signal and a sinusoid as:
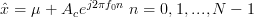. The complex dc level 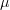and the sinusoidal amplitude 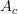are unknown and we are notified that we may view the determination of 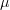, 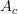as the solution of the overdetermined set of equations.
![\left[\begin{array}{cc}1 & 1 \\ 1 & e^{j2\pi f_{0}} \\ \vdots & \vdots \\ 1 & e^{j2\pi f_{0}(N-1)}\end{array} \right] \cdot \left[\begin{array}{c}\mu \\ A_{c} \end{array} \right] = \left[\begin{array}{c}x[0] \\ \vdots \\ x[N-1] \end{array} \right].](https://lysario.de/wp-content/cache/tex_bf7d1a9edfb68f8a07beb5ca2929cbc6.png) | (1) | ||
It is asked to find the least squares solution for
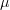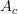and . If furthermore 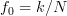, where 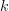is a nonzero integer in the range for even and for odd we are asked to determine again the least squares solution.
read the conclusion >
Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”,p. 34 exercise 2.12
Author: Panagiotis1 Apr
In [1, p. 34 exercise 2.12] we are asked to verify the equations given for the Cholesky decomposition, [1, (2.53)-(2.55)]. Furthermore it is requested to use these equations to find the inverse of the matrix given in problem [1, 2.7].
read the conclusion >