Lysario – by Panagiotis Chatzichrisafis
"ούτω γάρ ειδέναι το σύνθετον υπολαμβάνομεν, όταν ειδώμεν εκ τίνων και πόσων εστίν …"
Archive for Dezember, 2009
Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”,p. 34 exercise 2.8
Author: Panagiotis22 Dez
In exercise [1, p. 34 exercise 2.8] we are asked to find the inverse of the 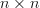 hermitian matrix
hermitian matrix  given by [1, (2.27)] by recursively applying Woodbury’s identity. This should be done by considering the cases where
given by [1, (2.27)] by recursively applying Woodbury’s identity. This should be done by considering the cases where 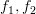 are arbitrary and where
are arbitrary and where 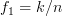 ,
, 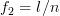 for
for 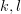 beeing distinct integers in the range
beeing distinct integers in the range ![\left[ -n/2,n/2-1 \right]](https://lysario.de/wp-content/cache/tex_349760367e158b72823c089231e45245.png) for
for  even and
even and ![\left[ -(n-1)/2,(n-1)/2 \right]](https://lysario.de/wp-content/cache/tex_bbbbf77ffaa65be463cde297b83e452b.png) for
for  odd.
read the conclusion >
odd.
read the conclusion >
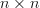 hermitian matrix
hermitian matrix  given by [1, (2.27)] by recursively applying Woodbury’s identity. This should be done by considering the cases where
given by [1, (2.27)] by recursively applying Woodbury’s identity. This should be done by considering the cases where 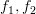 are arbitrary and where
are arbitrary and where 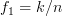 ,
, 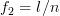 for
for 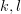 beeing distinct integers in the range
beeing distinct integers in the range ![\left[ -n/2,n/2-1 \right]](https://lysario.de/wp-content/cache/tex_349760367e158b72823c089231e45245.png) for
for  even and
even and ![\left[ -(n-1)/2,(n-1)/2 \right]](https://lysario.de/wp-content/cache/tex_bbbbf77ffaa65be463cde297b83e452b.png) for
for  odd.
read the conclusion >
odd.
read the conclusion >