Lysario – by Panagiotis Chatzichrisafis
"ούτω γάρ ειδέναι το σύνθετον υπολαμβάνομεν, όταν ειδώμεν εκ τίνων και πόσων εστίν …"
Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”,p. 35 exercise 2.16
Author: Panagiotis12 Aug
In [1, p. 35 exercise 2.16] we are asked to verify the formulas given for the complex gradient of a hermitian and a linear form [1, p. 31 (2.70)]. To do so, we are instructed to decompose the matrices and vectors into their real and imaginary parts as
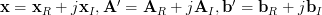
Solution: The formulas given by [1, p. 31 (2.70)] are
and
where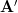 is a complex
is a complex 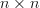 matrix with elements
matrix with elements 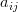 and
and 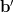 is a complex
is a complex 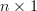 vector with elements
vector with elements 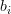 and
and 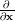 denotes the gradient of a real function in respect to
denotes the gradient of a real function in respect to
 . Although it is not explicitly stated (neither in the problem nor in the book text) the matrix must be hermitian for the two relations to hold. For Hermitian matrices one can obtain the following relations for the real (3) and imaginary (4) parts of the matrix:
. Although it is not explicitly stated (neither in the problem nor in the book text) the matrix must be hermitian for the two relations to hold. For Hermitian matrices one can obtain the following relations for the real (3) and imaginary (4) parts of the matrix:
A further relation which will be useful for the solution of the problem is the derivation of the formula of the gradient of a quadratic form of a real matrix which is not symmetric. We reproduce [2, rel. (4) from the solution of exercise 2.15] the formula for the real matrix![\mathbf{A}_{R} =[a_{ij}]](https://lysario.de/wp-content/cache/tex_db2a1f23e84b47a5881f12f49781d31a.png) and the real vector
and the real vector ![\mathbf{x}_{R}=[x_{i}]](https://lysario.de/wp-content/cache/tex_efcab38f639e50fac5f59b6b3d91ea9b.png) :
:
And thus
The last relation is a general expression of the gradient of a real matrix. Expanding the term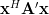 by using the real and imaginary parts we obtain:
by using the real and imaginary parts we obtain:
Using the definition of the complex gradient ([1, p. 32 (2.69)])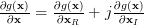 we have to calculate the partial derivatives in respect to
we have to calculate the partial derivatives in respect to 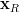 and
and 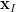 :
:
and because of (3,4) we obtain the relation
Similar the gradient to the imaginary part of is obtained by
is obtained by
and because of (3,4) we obtain the relation
From (6) and (7) we obtain using the definition of the complex gradian:
Equation 11 proofs the first part of equations [1, p. 31 (2.70)]. The second equation can be solved similar by setting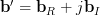 and thus:
and thus:
The gradient of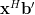 in respect to the real and imaginary part of
in respect to the real and imaginary part of  is obtained by:
is obtained by:
while the gradient of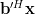 in respect to the real and imaginary part of
in respect to the real and imaginary part of  is given by
is given by
From the previous relations we obtain:
which can be used to find the complex gradient using its definition ([1, p. 32 (2.69)])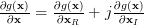 :
:
The result (10) proofs the second part of the equations [1, p. 31 (2.70)]. QED.
[1] Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”, Prentice Hall, ISBN: 0-13-598582-X.
[2] Chatzichrisafis: “Solution of exercise 2.15 from Kay’s Modern Spectral Estimation - Theory and Applications”.
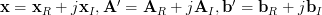
Solution: The formulas given by [1, p. 31 (2.70)] are
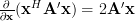 | (1) | ||
and
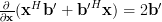 | (2) | ||
where
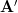 is a complex
is a complex 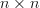 matrix with elements
matrix with elements 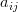 and
and 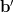 is a complex
is a complex 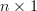 vector with elements
vector with elements 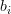 and
and 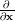 denotes the gradient of a real function in respect to
denotes the gradient of a real function in respect to
 . Although it is not explicitly stated (neither in the problem nor in the book text) the matrix must be hermitian for the two relations to hold. For Hermitian matrices one can obtain the following relations for the real (3) and imaginary (4) parts of the matrix:
. Although it is not explicitly stated (neither in the problem nor in the book text) the matrix must be hermitian for the two relations to hold. For Hermitian matrices one can obtain the following relations for the real (3) and imaginary (4) parts of the matrix:
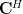 |  | 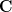 | |
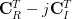 |  | 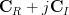 | |
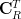 |  | 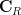 | (3) |
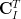 |  | 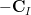 | (4) |
A further relation which will be useful for the solution of the problem is the derivation of the formula of the gradient of a quadratic form of a real matrix which is not symmetric. We reproduce [2, rel. (4) from the solution of exercise 2.15] the formula for the real matrix
![\mathbf{A}_{R} =[a_{ij}]](https://lysario.de/wp-content/cache/tex_db2a1f23e84b47a5881f12f49781d31a.png) and the real vector
and the real vector ![\mathbf{x}_{R}=[x_{i}]](https://lysario.de/wp-content/cache/tex_efcab38f639e50fac5f59b6b3d91ea9b.png) :
:
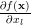 |  | 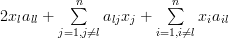 | |
 | 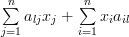 |
And thus
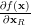 |  | 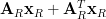 |
The last relation is a general expression of the gradient of a real matrix. Expanding the term
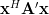 by using the real and imaginary parts we obtain:
by using the real and imaginary parts we obtain:
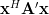 |  | 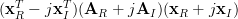 | |
 | 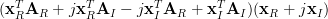 | ||
 | 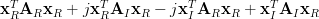 | ||
 | 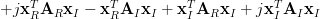 | ||
 | 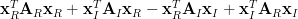 | ||
 | 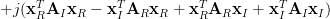 | (5) |
Using the definition of the complex gradient ([1, p. 32 (2.69)])
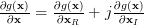 we have to calculate the partial derivatives in respect to
we have to calculate the partial derivatives in respect to 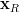 and
and 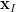 :
:
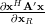 |  | 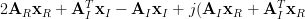 | |
 | 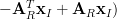 |
and because of (3,4) we obtain the relation
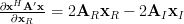 | (6) | ||
Similar the gradient to the imaginary part of
 is obtained by
is obtained by
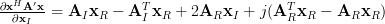 | |||
and because of (3,4) we obtain the relation
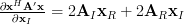 | (7) | ||
From (6) and (7) we obtain using the definition of the complex gradian:
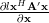 |  | 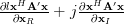 | |
 | 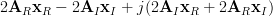 | ||
 | 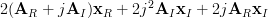 | ||
 | 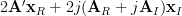 | ||
 | 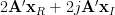 | ||
 | 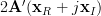 | ||
 | 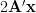 | (11) |
Equation 11 proofs the first part of equations [1, p. 31 (2.70)]. The second equation can be solved similar by setting
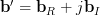 and thus:
and thus:
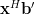 |  | 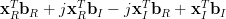 | (8) |
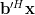 |  | 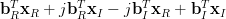 | (9) |
The gradient of
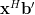 in respect to the real and imaginary part of
in respect to the real and imaginary part of  is obtained by:
is obtained by:
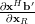 |  | 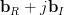 | |
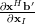 |  | 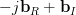 |
while the gradient of
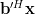 in respect to the real and imaginary part of
in respect to the real and imaginary part of  is given by
is given by
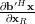 |  | 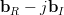 | |
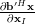 |  | 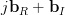 |
From the previous relations we obtain:
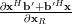 |  | 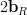 | |
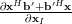 |  | 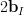 |
which can be used to find the complex gradient using its definition ([1, p. 32 (2.69)])
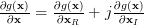 :
:
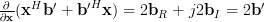 | (10) | ||
The result (10) proofs the second part of the equations [1, p. 31 (2.70)]. QED.
[1] Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”, Prentice Hall, ISBN: 0-13-598582-X.
[2] Chatzichrisafis: “Solution of exercise 2.15 from Kay’s Modern Spectral Estimation - Theory and Applications”.
Leave a reply