Lysario – by Panagiotis Chatzichrisafis
"ούτω γάρ ειδέναι το σύνθετον υπολαμβάνομεν, όταν ειδώμεν εκ τίνων και πόσων εστίν …"
Archive for Mai, 2013
Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”,p. 62 exercise 3.19
Author: Panagiotis17 Mai
In [1, p. 62 exercise 3.19] we are asked to find for the multiple sinusoidal process
the ensemble ACF and the temporal ACF as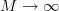 , where the
, where the 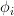 ‘s are all uniformly distributed random variables on
‘s are all uniformly distributed random variables on 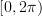 and independent of each other. We are also asked to determine if this random process is autocorrelation ergodic.
read the conclusion >
and independent of each other. We are also asked to determine if this random process is autocorrelation ergodic.
read the conclusion >
![x[n]=\sum\limits_{i=1}^{P}A_{i}\cos(2\pi f_{i}n+\phi_{i})](https://lysario.de/wp-content/cache/tex_18c06f6747166204af88405a37dafba0.png) | |||
the ensemble ACF and the temporal ACF as
 , where the
, where the 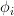 ‘s are all uniformly distributed random variables on
‘s are all uniformly distributed random variables on 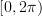 and independent of each other. We are also asked to determine if this random process is autocorrelation ergodic.
read the conclusion >
and independent of each other. We are also asked to determine if this random process is autocorrelation ergodic.
read the conclusion >