Lysario – by Panagiotis Chatzichrisafis
"ούτω γάρ ειδέναι το σύνθετον υπολαμβάνομεν, όταν ειδώμεν εκ τίνων και πόσων εστίν …"
Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”,p. 35 exercise 2.18
Author: Panagiotis22 Aug
In [1, p. 35 exercise 2.18] we are asked to prove that the inverse of a complex matrix 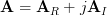 may be found by first inverting
may be found by first inverting
to yield
and then letting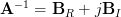 .
.
Solution: From the information that (2) is the inverse of (1) we can obtain the relations:
which can be reduced to :
Computing the product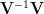 will result in:
will result in:
and the relations that can be obtained by the previous equation can be reduced to :
Now we will proceed to show that the inverse of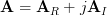 is
is 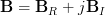 .
First we will proof that
.
First we will proof that 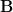 is the right inverse
of
is the right inverse
of  :
:
The last relation is obtained by considering (3) and (4). Next we will show that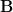 is also the left inverse of
is also the left inverse of  :
:
The last relation is obtained by considering (5) and (6). Thus the matrix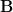 is the inverse of the matrix
is the inverse of the matrix  . QED.
. QED.
[1] Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”, Prentice Hall, ISBN: 0-13-598582-X.
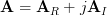 may be found by first inverting
may be found by first inverting
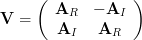 | (1) | ||
to yield
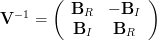 | (2) | ||
and then letting
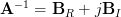 .
.
Solution: From the information that (2) is the inverse of (1) we can obtain the relations:
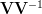 |  | 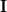 | |
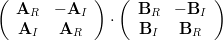 |  | 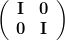 | |
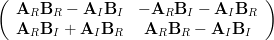 |  | 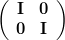 |
which can be reduced to :
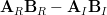 |  | 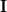 | (3) |
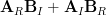 |  | 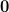 | (4) |
Computing the product
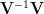 will result in:
will result in:
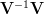 |  | 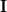 | |
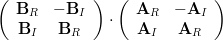 |  | 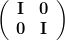 | |
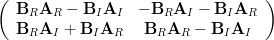 |  | 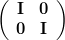 |
and the relations that can be obtained by the previous equation can be reduced to :
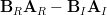 |  | 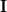 | (5) |
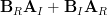 |  | 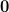 | (6) |
Now we will proceed to show that the inverse of
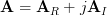 is
is 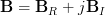 .
First we will proof that
.
First we will proof that 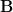 is the right inverse
of
is the right inverse
of  :
:
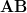 |  | 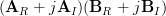 | |
 | 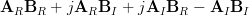 | ||
 | 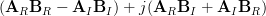 | ||
 | 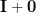 |
The last relation is obtained by considering (3) and (4). Next we will show that
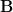 is also the left inverse of
is also the left inverse of  :
:
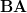 |  | 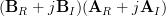 | |
 | 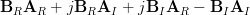 | ||
 | 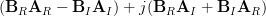 | ||
 | 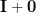 |
The last relation is obtained by considering (5) and (6). Thus the matrix
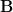 is the inverse of the matrix
is the inverse of the matrix  . QED.
. QED.
[1] Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”, Prentice Hall, ISBN: 0-13-598582-X.
Leave a reply