Lysario – by Panagiotis Chatzichrisafis
"ούτω γάρ ειδέναι το σύνθετον υπολαμβάνομεν, όταν ειδώμεν εκ τίνων και πόσων εστίν …"
Archive for August, 2010
Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”,p. 35 exercise 2.18
Author: Panagiotis22 Aug
In [1, p. 35 exercise 2.18] we are asked to prove that the inverse of a complex matrix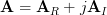 
may be found by first inverting
to yield
and then letting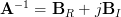
.
read the conclusion >
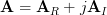may be found by first inverting
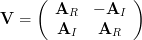 | (1) | ||
to yield
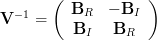 | (2) | ||
and then letting
.
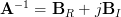read the conclusion >
Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”,p. 35 exercise 2.17
Author: Panagiotis16 Aug
In [1, p. 35 exercise 2.17] we are asked to verify the alternative expression [1, p. 33 (2.77)] for a hermitian function.
read the conclusion >
Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”,p. 35 exercise 2.16
Author: Panagiotis12 Aug
In [1, p. 35 exercise 2.16] we are asked to verify the formulas given for the complex gradient of a hermitian and a linear form [1, p. 31 (2.70)]. To do so, we are instructed to decompose the matrices and vectors into their real and imaginary parts as
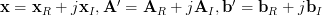read the conclusion >
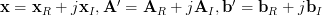read the conclusion >