Lysario – by Panagiotis Chatzichrisafis
"ούτω γάρ ειδέναι το σύνθετον υπολαμβάνομεν, όταν ειδώμεν εκ τίνων και πόσων εστίν …"
Archive for Februar, 2014
Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”,p. 94 exercise 4.1
Author: Panagiotis1 Feb
In problem [1, p. 94 exercise 4.1] we will show that the periodogram is an inconsistent estimator by examining the estimator at 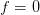 , or
, or
If![x[n]](https://lysario.de/wp-content/cache/tex_d3baaa3204e2a03ef9528a7d631a4806.png) is real white Gaussian noise process with PSD
is real white Gaussian noise process with PSD
we are asked to find the mean an variance of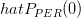 . We are asked if the variance converge to zero as
. We are asked if the variance converge to zero as 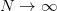 . The hint provided within the exercise is to note that
. The hint provided within the exercise is to note that
where the quantiiy inside the parenthesis is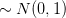 read the conclusion >
read the conclusion >
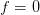 , or
, or
![\hat{P}_{PER}(0)=\frac{1}{N}\left(\sum\limits_{n=0}^{N-1}x[n]\right)^{2}.](https://lysario.de/wp-content/cache/tex_938765f09480f77020c3aad219444ca0.png) | (1) | ||
If
![x[n]](https://lysario.de/wp-content/cache/tex_d3baaa3204e2a03ef9528a7d631a4806.png) is real white Gaussian noise process with PSD
is real white Gaussian noise process with PSD
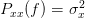 | (2) | ||
we are asked to find the mean an variance of
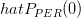 . We are asked if the variance converge to zero as
. We are asked if the variance converge to zero as 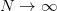 . The hint provided within the exercise is to note that
. The hint provided within the exercise is to note that
![\hat{P}_{PER}(0)= \sigma_{x}^{2} \left(\sum\limits_{n=0}^{N-1}\frac{x[n]}{\sigma_{x}\sqrt{N}}\right)^{2}](https://lysario.de/wp-content/cache/tex_df83a5d6a6944d47bfd3d103cb81d6c4.png) | (3) | ||
where the quantiiy inside the parenthesis is
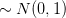 read the conclusion >
read the conclusion >