Lysario – by Panagiotis Chatzichrisafis
"ούτω γάρ ειδέναι το σύνθετον υπολαμβάνομεν, όταν ειδώμεν εκ τίνων και πόσων εστίν …"
Archive for Juni, 2014
Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”,p. 94 exercise 4.2
Author: Panagiotis24 Jun
In [1, p. 94 exercise 4.2] we are asked to consider the estimator
where
for the process of Problem 4.1. We are informed that this estimator may be viewed as an averaged periodogram. In this point of view the data record is sectioned into blocks (in this case, of length 1) and the periodograms for each block are averaged. We are asked to find the mean and variance of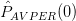
and compare the result to that obtained in [2].
read the conclusion >
 | (1) | ||
where
![\hat{P}_{PER}^{m}(0)= x^{2}[m]](https://lysario.de/wp-content/cache/tex_111f972a11d36418820c12baa2503f8a.png) | (2) | ||
for the process of Problem 4.1. We are informed that this estimator may be viewed as an averaged periodogram. In this point of view the data record is sectioned into blocks (in this case, of length 1) and the periodograms for each block are averaged. We are asked to find the mean and variance of
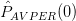and compare the result to that obtained in [2].
read the conclusion >