Lysario – by Panagiotis Chatzichrisafis
"ούτω γάρ ειδέναι το σύνθετον υπολαμβάνομεν, όταν ειδώμεν εκ τίνων και πόσων εστίν …"
Archive for the ‘Kay: Modern Spectral Estimation, Theory and Application’ Category
Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”,p. 61 exercise 3.6
Author: Panagiotis19 Apr
In [1, p. 61 exercise 3.6] we are asked to assume that the variance is to be estimated as well as the mean for the conditions of [1, p. 60 exercise 3.4] (see also [2, solution of exercise 3.4]) . We are asked to prove for the vector parameter ![\mathbf{\theta}=\left[\mu_x \; \sigma^2_x\right]^T](https://lysario.de/wp-content/cache/tex_b1d973967798bb8525bff936468f9211.png)
, that the Fisher information matrix is
Furthermore we are asked to find the CR bound and to determine if the sample mean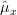
is efficient.
If additionaly the variance is to be estimated as
then we are asked to determine if this estimator is unbiased and efficient. Hint: We are instructed to use the result that
read the conclusion >
, that the Fisher information matrix is
![\mathbf{I}_{\theta}=\left[\begin{array}{cc} \frac{N}{\sigma^2_x} & 0 \\ 0 & \frac{N}{2\sigma^4_x} \end{array}\right]](https://lysario.de/wp-content/cache/tex_42789b24f24a6a32db03314ccac291c8.png) | |||
Furthermore we are asked to find the CR bound and to determine if the sample mean
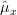is efficient.
If additionaly the variance is to be estimated as
![\hat{\sigma}^2_x=\frac{1}{N-1}\sum\limits_{n=0}^{N-1}(x[n]-\hat{\mu}_x)^2](https://lysario.de/wp-content/cache/tex_13d6ef5f9b8f0b1d9832efd9b58af88b.png) | |||
then we are asked to determine if this estimator is unbiased and efficient. Hint: We are instructed to use the result that
 | |||
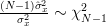read the conclusion >
Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”,p. 61 exercise 3.5
Author: Panagiotis11 Jan
In [1, p. 61 exercise 3.5] we are asked to show that for the conditions of Problem [1, p. 60, exercise 3.4] the CR bound is
and further to give a statement about the efficiency of the sample mean estimator. read the conclusion >
 | |||
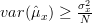and further to give a statement about the efficiency of the sample mean estimator. read the conclusion >
Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”,p. 60 exercise 3.4
Author: Panagiotis28 Dez
In [1, p. 60 exercise 3.4] we are asked to prove that the estimate
is an unbiased estimator, given![\left\{x[0],x[1],...,x[N]\right\}](https://lysario.de/wp-content/cache/tex_1cc48dbb4a4db05229880d4eafd1756b.png)
are independent and identically distributed according to a 
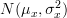distribution. Furthermore we are asked to also find the variance of the estimator.
read the conclusion >
![\hat{\mu}_x = \frac{1}{N}\sum\limits^{N-1}_{n=0}x[n]](https://lysario.de/wp-content/cache/tex_fdf7f47786a09a823706c0185f0d813a.png) | (1) | ||
is an unbiased estimator, given
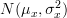are independent and identically distributed according to a distribution. Furthermore we are asked to also find the variance of the estimator.
read the conclusion >
Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”,p. 60 exercise 3.3
Author: Panagiotis4 Dez
In [1, p. 60 exercise 3.3] we are asked to prove that the complex multivariate Gaussian PDF reduces to the complex univariate Gaussian PDF if N=1.
read the conclusion >
Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”,p. 60 exercise 3.2
Author: Panagiotis8 Nov
In [1, p. 60 exercise 3.2] we are asked to proof by using the method of characteristic functions that the sum of squares of N independent and identically distributed N(0,1) random variables has a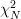 
distribution. read the conclusion >
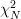distribution. read the conclusion >