Lysario – by Panagiotis Chatzichrisafis
"ούτω γάρ ειδέναι το σύνθετον υπολαμβάνομεν, όταν ειδώμεν εκ τίνων και πόσων εστίν …"
Archive for the ‘Solved Problems’ Category
Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”,p. 61 exercise 3.11
Author: Panagiotis29 Jan
In [1, p. 61 exercise 3.11] it is asked to repeat problem [1, p. 61 exercise 3.10] (see also the solution [2] ) for the general case when the predictor is given as
Furthermore we are asked to show that the optimal prediction coefficients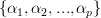
are found by solving [1, p. 157, eq. 6.4 ] and the minimum prediction error power is given by [1, p. 157, eq. 6.5 ].
read the conclusion >
![\hat{x}[n]=-\sum\limits_{k=1}^{p}\alpha_{k}x[n-k].](https://lysario.de/wp-content/cache/tex_e9899bf3e42bcb01eecd9ca3794e97db.png) | (1) | ||
Furthermore we are asked to show that the optimal prediction coefficients
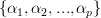are found by solving [1, p. 157, eq. 6.4 ] and the minimum prediction error power is given by [1, p. 157, eq. 6.5 ].
read the conclusion >
Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”,p. 61 exercise 3.10
Author: Panagiotis23 Jan
The desire to predict the complex WSS random process based on the sample ![x[n-1]](https://lysario.de/wp-content/cache/tex_f14c06cc1753ec7fe07c98dd3f429390.png)
by using a linear predictor
is expressed in [1, p. 61 exercise 3.10]. It is asked to chose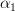
to minimize the MSE or prediction error power
We are asked to find the optimal prediction parameter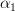 and the minimum prediction error power by using the orthogonality principle.
read the conclusion >
by using a linear predictor
![\hat{x}[n]=-\alpha_{1}x[n-1]](https://lysario.de/wp-content/cache/tex_3edb3496c7a3a354e025c6fc6946e035.png) | (1) | ||
is expressed in [1, p. 61 exercise 3.10]. It is asked to chose
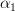to minimize the MSE or prediction error power
![MSE = \mathcal{E}\left\{\left| x[n] -\hat{x}[n] \right|^{2} \right\}.](https://lysario.de/wp-content/cache/tex_108f20c754ba9aebb9393528fd95ffae.png) | (2) | ||
We are asked to find the optimal prediction parameter
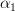and the minimum prediction error power by using the orthogonality principle. read the conclusion >
Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”,p. 61 exercise 3.9
Author: Panagiotis3 Jan
In [1, p. 61 exercise 3.9] we are asked to consider the real linear model
and find the MLE of the slope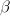
and the intercept 
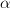by assuming that ![z[n]](https://lysario.de/wp-content/cache/tex_8a8c996b9e9d1294c8f815911479257f.png)
is real white Gaussian noise with mean zero and variance 
.
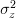Furthermore it is requested to find the MLE of 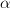if in the linear model we set 
.
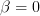read the conclusion >
![x[n]=\alpha + \beta n + z[n] \; n=0,1,...,N-1](https://lysario.de/wp-content/cache/tex_b693a80228f813c59eb716ad50e93b09.png) | (1) | ||
and find the MLE of the slope
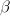and the intercept 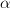by assuming that is real white Gaussian noise with mean zero and variance .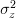
Furthermore it is requested to find the MLE of 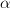if in the linear model we set .
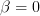read the conclusion >
Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”,p. 61 exercise 3.8
Author: Panagiotis22 Sep
In [1, p. 61 exercise 3.8] we are asked to prove that the sample mean is a sufficient statistic for the mean under the conditions of [1, p. 61 exercise 3.4].
Assuming that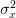 
is known. We are asked to find the MLE of the mean by maximizing 
.
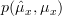read the conclusion >
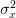is known. We are asked to find the MLE of the mean by maximizing .
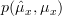read the conclusion >
Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”,p. 61 exercise 3.7
Author: Panagiotis25 Apr
In [1, p. 61 exercise 3.7] we are asked to find the MLE of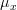 
and 
.
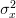for the conditions of Problem [1, p. 60 exercise 3.4] (see also [2, solution of exercise 3.4]).
We are asked if the MLE of the parameters are asymptotically unbiased , efficient and Gaussianly distributed.
read the conclusion >
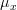and .
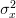for the conditions of Problem [1, p. 60 exercise 3.4] (see also [2, solution of exercise 3.4]).
We are asked if the MLE of the parameters are asymptotically unbiased , efficient and Gaussianly distributed. read the conclusion >