Lysario – by Panagiotis Chatzichrisafis
"ούτω γάρ ειδέναι το σύνθετον υπολαμβάνομεν, όταν ειδώμεν εκ τίνων και πόσων εστίν …"
Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”,p. 61 exercise 3.9
Author: Panagiotis3 Jan
In [1, p. 61 exercise 3.9] we are asked to consider the real linear model
and find the MLE of the slope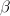 and the intercept
and the intercept 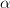 by assuming that
by assuming that ![z[n]](https://lysario.de/wp-content/cache/tex_8a8c996b9e9d1294c8f815911479257f.png) is real white Gaussian noise with mean zero and variance
is real white Gaussian noise with mean zero and variance 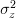 .
Furthermore it is requested to find the MLE of
.
Furthermore it is requested to find the MLE of 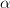 if in the linear model we set
if in the linear model we set 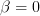 .
.
Solution: The probability distribution function of the Gaussian variable
with mean zero and variance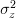 is given by
is given by
The MLE estimator can be found by finding the minimum for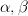 of the exponent:
of the exponent:
The gradient of the exponent is equal to :
In order to obtain an extremum the gradient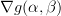 has to become zero. Thus
has to become zero. Thus
Using [2, p. 980, E-4, 1.]: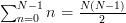 and [2, p. 980, E-4, 5.]:
and [2, p. 980, E-4, 5.]: 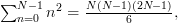 (6) can be written as:
(6) can be written as:
From (7) we obtain the following solutions for the intercept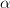 and the slope
and the slope 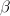 , for
, for 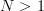 :
:
If the slope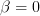 the LE equation becomes by the same reasoning
the LE equation becomes by the same reasoning
The ML solution for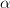 is then
is then
![\alpha =\frac{1}{N}\sum_{n=0}^{N-1}x[n].](https://lysario.de/wp-content/cache/tex_d517c5d6e34aa4a70b737a7cab3774fb.png)
[1] Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”, Prentice Hall, ISBN: 0-13-598582-X.
[2] Granino A. Korn and Theresa M. Korn: “Mathematical Handbook for Scientists and Engineers”, Dover, ISBN: 978-0-486-41147-7.
![x[n]=\alpha + \beta n + z[n] \; n=0,1,...,N-1](https://lysario.de/wp-content/cache/tex_b693a80228f813c59eb716ad50e93b09.png) | (1) | ||
and find the MLE of the slope
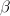 and the intercept
and the intercept 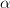 by assuming that
by assuming that ![z[n]](https://lysario.de/wp-content/cache/tex_8a8c996b9e9d1294c8f815911479257f.png) is real white Gaussian noise with mean zero and variance
is real white Gaussian noise with mean zero and variance 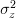 .
Furthermore it is requested to find the MLE of
.
Furthermore it is requested to find the MLE of 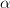 if in the linear model we set
if in the linear model we set 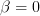 .
.
Solution: The probability distribution function of the Gaussian variable
![z[n]=x[n]-\alpha-\beta n](https://lysario.de/wp-content/cache/tex_c619baa17d95f5772748849dc680c10c.png) | (2) | ||
with mean zero and variance
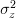 is given by
is given by
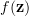 |  | 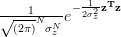 | |
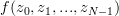 |  | 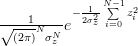 | |
| (3) | |||
The MLE estimator can be found by finding the minimum for
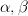 of the exponent:
of the exponent:
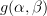 |  | 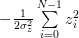 | |
 | ![-\frac{1}{2\sigma^{2}_{z}} \sum\limits_{n=0}^{N-1}(x[n]-\alpha-\beta n)^{2}](https://lysario.de/wp-content/cache/tex_ad70cd13a7e2e87541c466270a494c26.png) | (4) |
The gradient of the exponent is equal to :
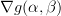 |  | ![\left[ \begin{array}{cc} \frac{\partial g(\alpha,\beta)}{\partial \alpha} & \frac{\partial g(\alpha,\beta)}{\partial \beta} \end{array}\right] ^{T}](https://lysario.de/wp-content/cache/tex_8578a2a348843f10f9d22eb791acb606.png) | |
 | ![\left[ \begin{array}{cc} \frac{\sum\limits_{n=0}^{N-1}(x[n]-\alpha-\beta n)}{\sigma_{z}^{2}}& \frac{\sum\limits_{n=0}^{N-1}(x[n] n-\alpha n-\beta n^{2})}{\sigma_{z}^{2}} \end{array}\right] ^{T}](https://lysario.de/wp-content/cache/tex_13d49399942fedb783d8e0da3c87c563.png) | (5) |
In order to obtain an extremum the gradient
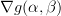 has to become zero. Thus
has to become zero. Thus
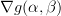 |  |  | |
![\left[ \begin{array}{c} {\sum\limits_{n=0}^{N-1}(x[n]-\alpha-\beta n)} \\ {\sum\limits_{n=0}^{N-1}(x[n] n-\alpha n-\beta n^{2})} \end{array}\right]](https://lysario.de/wp-content/cache/tex_477e9c13700dcb51c51d592fa43f5e3b.png) |  |  | |
![\left[ \begin{array}{c}N \alpha + \beta \sum\limits_{n=0}^{N-1}n \\ \alpha \sum\limits_{n=0}^{N-1}n +\beta \sum\limits_{n=0}^{N-1}n^{2} \end{array}\right]](https://lysario.de/wp-content/cache/tex_215178353300132830b14f584d3aedb5.png) |  | ![\left[ \begin{array}{c} {\sum\limits_{n=0}^{N-1}x[n]} \\ {\sum\limits_{n=0}^{N-1}(x[n] n)} \end{array}\right]](https://lysario.de/wp-content/cache/tex_353976e5c4fd477a5bb53e9ac800ad1e.png) | |
![\left[ \begin{array}{cc}N & \sum\limits_{n=0}^{N-1}n \\ \sum\limits_{n=0}^{N-1}n & \sum\limits_{n=0}^{N-1}n^{2} \end{array}\right] \left[ \begin{array}{c} \alpha \\ \beta \end{array}\right]](https://lysario.de/wp-content/cache/tex_632c33c40c269a3284d2721852c45fae.png) |  | ![\left[ \begin{array}{c} {\sum\limits_{n=0}^{N-1}x[n]} \\ {\sum\limits_{n=0}^{N-1}(x[n] n)} \end{array}\right]](https://lysario.de/wp-content/cache/tex_353976e5c4fd477a5bb53e9ac800ad1e.png) | (6) |
Using [2, p. 980, E-4, 1.]:
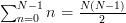 and [2, p. 980, E-4, 5.]:
and [2, p. 980, E-4, 5.]: 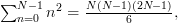 (6) can be written as:
(6) can be written as:
![\left[ \begin{array}{cc}N & \frac{N(N-1)}{2} \\ \frac{N(N-1)}{2} & \frac{N(N-1)(2N-1)}{6} \end{array}\right] \left[ \begin{array}{c} \alpha \\ \beta \end{array}\right]](https://lysario.de/wp-content/cache/tex_9f82b02c5851dbc01bcc85fcd6db7e9f.png) |  | ![\left[ \begin{array}{c} {\sum\limits_{n=0}^{N-1}x[n]} \\ {\sum\limits_{n=0}^{N-1}(x[n] n)} \end{array}\right]](https://lysario.de/wp-content/cache/tex_353976e5c4fd477a5bb53e9ac800ad1e.png) | (7) |
From (7) we obtain the following solutions for the intercept
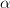 and the slope
and the slope 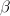 , for
, for 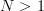 :
:
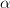 |  | ![%12 \frac{N(N-1)}{2}\frac{\frac{2N-1}{3}(\sum\limits\limits_{n=0}^{N-1}x[n])-(\sum\limits_{n=0}^{N-1}nx[n])}{N^{2}(N+1)(N-1)}
6 \cdot \frac{\frac{2N-1}{3}(\sum\limits\limits_{n=0}^{N-1}x[n])-(\sum\limits_{n=0}^{N-1}nx[n])}{N(N+1)}](https://lysario.de/wp-content/cache/tex_02afa703828a55a4361d2ddecc41ae84.png) | (8) |
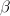 |  | ![%12 \frac{N \sum\limits\limits_{n=0}^{N-1}(nx[n])-\frac{N(N-1)}{2}\sum\limits\limits_{n=0}^{N-1}x[n]}{N^{2}(N+1)(N-1)}
6 \cdot \frac{ 2 \sum\limits\limits_{n=0}^{N-1}(nx[n])-(N-1)\sum\limits\limits_{n=0}^{N-1}x[n]}{N(N+1)(N-1)}](https://lysario.de/wp-content/cache/tex_e8754427a96f0ef7f39d687ed8f6d149.png) | (9) |
If the slope
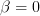 the LE equation becomes by the same reasoning
the LE equation becomes by the same reasoning
![\sum\limits_{n=0}^{N-1}(x[n]-a)](https://lysario.de/wp-content/cache/tex_eb8dff54dae5e58c43ca0cb7f8d0d2bf.png) |  | 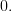 | (10) |
The ML solution for
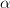 is then
is then ![\alpha =\frac{1}{N}\sum_{n=0}^{N-1}x[n].](https://lysario.de/wp-content/cache/tex_d517c5d6e34aa4a70b737a7cab3774fb.png)
[1] Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”, Prentice Hall, ISBN: 0-13-598582-X.
[2] Granino A. Korn and Theresa M. Korn: “Mathematical Handbook for Scientists and Engineers”, Dover, ISBN: 978-0-486-41147-7.
Leave a reply