Lysario – by Panagiotis Chatzichrisafis
"ούτω γάρ ειδέναι το σύνθετον υπολαμβάνομεν, όταν ειδώμεν εκ τίνων και πόσων εστίν …"
Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”,p. 61 exercise 3.10
Author: Panagiotis23 Jan
The desire to predict the complex WSS random process based on the sample ![x[n-1]](https://lysario.de/wp-content/cache/tex_f14c06cc1753ec7fe07c98dd3f429390.png) by using a linear predictor
by using a linear predictor
is expressed in [1, p. 61 exercise 3.10]. It is asked to chose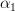 to minimize the MSE or prediction error power
to minimize the MSE or prediction error power
We are asked to find the optimal prediction parameter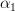 and the minimum prediction error power by using the orthogonality principle.
and the minimum prediction error power by using the orthogonality principle.
Solution: Using the orthogonality principle [1, p.51, eq. 3.38] for the estimation of![x[n]](https://lysario.de/wp-content/cache/tex_d3baaa3204e2a03ef9528a7d631a4806.png) translates into finding the
translates into finding the 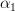 for which the observed data
for which the observed data ![x[n-1]](https://lysario.de/wp-content/cache/tex_f14c06cc1753ec7fe07c98dd3f429390.png) will be normal to the error
will be normal to the error
Considering (3), the mean squared error can be written as:
This result can also be obtained by the equations [1, eq. 3.36, eq. 3.37]. They provide the solution for the optimal prediction parameter of a linear predictor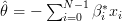 , that minimizes the MSE and the minimum MSE. Note that in the book
, that minimizes the MSE and the minimum MSE. Note that in the book 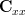 is used instead of
is used instead of 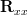 and
and 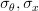 instead of
instead of ![r_{\theta \theta}[0]](https://lysario.de/wp-content/cache/tex_c0219a326d69241fe834eb6473323994.png) and
and ![r_{xx}[0]](https://lysario.de/wp-content/cache/tex_92c5630642b279858745d05d4097b3fc.png) . This is only correct for a zero mean random process
. This is only correct for a zero mean random process ![x[n]](https://lysario.de/wp-content/cache/tex_d3baaa3204e2a03ef9528a7d631a4806.png) , as it is assumed in the derivation of the formula in the book. The formula for the optimal coefficients is thus:
, as it is assumed in the derivation of the formula in the book. The formula for the optimal coefficients is thus:
The minimum MSE is for a general signal![x[n]](https://lysario.de/wp-content/cache/tex_d3baaa3204e2a03ef9528a7d631a4806.png) is equal to:
is equal to:
Translating the formulas to the notation of the exercise, we obtain![\theta =x[n]](https://lysario.de/wp-content/cache/tex_ebceea97dfa3ecda473bc59100754274.png) ,
,![\mathbf{x}=x[n-1]](https://lysario.de/wp-content/cache/tex_fe89bc16cb2f5f0ba3baf853dd3118a7.png) ,
, 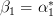 and
and ![\mathbf{r}_{\theta x}=E\left\{\mathbf{x}\theta^{H}\right\}=E\left\{x^{\ast}[n]x[n-1]\right\}=r_{xx}[-1]](https://lysario.de/wp-content/cache/tex_fea96e545397b9f1724990fedcc117e0.png) ,
, ![\mathbf{R}_{xx}=E\left\{ x^{\ast}[n-1]x[n-1]\right\}=r_{xx}[0]](https://lysario.de/wp-content/cache/tex_b0865d4540df90fe1b90e211dd8a9da5.png) and for a zero mean process
and for a zero mean process ![r_{xx}[0]=\sigma_{\theta}^{2}=\sigma_{x}^{2}](https://lysario.de/wp-content/cache/tex_23b9fa5525a8d3c398f88495687c81bb.png) .
The optimal prediction parameter
.
The optimal prediction parameter 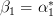 is thus given by:
is thus given by:
while the minimum MSE is given by:
Which is equal to the solution that was obtained using the orthogonality principle (4).
[1] Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”, Prentice Hall, ISBN: 0-13-598582-X.
![x[n-1]](https://lysario.de/wp-content/cache/tex_f14c06cc1753ec7fe07c98dd3f429390.png) by using a linear predictor
by using a linear predictor
![\hat{x}[n]=-\alpha_{1}x[n-1]](https://lysario.de/wp-content/cache/tex_3edb3496c7a3a354e025c6fc6946e035.png) | (1) | ||
is expressed in [1, p. 61 exercise 3.10]. It is asked to chose
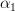 to minimize the MSE or prediction error power
to minimize the MSE or prediction error power
![MSE = \mathcal{E}\left\{\left| x[n] -\hat{x}[n] \right|^{2} \right\}.](https://lysario.de/wp-content/cache/tex_108f20c754ba9aebb9393528fd95ffae.png) | (2) | ||
We are asked to find the optimal prediction parameter
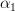 and the minimum prediction error power by using the orthogonality principle.
and the minimum prediction error power by using the orthogonality principle. Solution: Using the orthogonality principle [1, p.51, eq. 3.38] for the estimation of
![x[n]](https://lysario.de/wp-content/cache/tex_d3baaa3204e2a03ef9528a7d631a4806.png) translates into finding the
translates into finding the 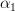 for which the observed data
for which the observed data ![x[n-1]](https://lysario.de/wp-content/cache/tex_f14c06cc1753ec7fe07c98dd3f429390.png) will be normal to the error
will be normal to the error
![E\left\{ x[n-1]\left(x[n]+a_{1}x[n-1]\right)^{H}\right\}](https://lysario.de/wp-content/cache/tex_b334af5ffd2493ebeb3000190a48a699.png) |  | 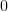 | |
![r_{xx}[-1]+a^{\ast}_{1}r_{xx}[0]](https://lysario.de/wp-content/cache/tex_f80deb40ec1b806715d26cbf91dbf9cd.png) |  | 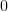 | |
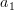 |  | ![-\frac{r^{\ast}_{xx}[-1]}{r_{xx}[0]}.](https://lysario.de/wp-content/cache/tex_d3c17a4c19038e5929a014694011dfc0.png) | (3) |
Considering (3), the mean squared error can be written as:
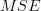 |  | ![E\left\{(x[n]+a_{1}x[n-1])(x[n]+a_{1}x[n-1])^{\ast}\right\}](https://lysario.de/wp-content/cache/tex_058a8fd70f430ce9f06219b6be812f68.png) | |
 | ![r_{xx}[0]+a_{1}r_{xx}[-1]+a^{\ast}_{1}r_{xx}[1]+|a_{1}|^{2}r_{xx}[0]](https://lysario.de/wp-content/cache/tex_65ca812154640454474ab7d7f202832b.png) | ||
 | ![r_{xx}[0]+a_{1}r_{xx}[-1]+a^{\ast}_{1}r^{\ast}_{xx}[-1]+|a_{1}|^{2}r_{xx}[0]](https://lysario.de/wp-content/cache/tex_72115f6892c928dc8b2b2d80f864b1ee.png) | ||
 | ![r_{xx}[0]- \frac{|r_{xx}[-1]|^{2}}{r_{xx}[0]}-\frac{|r_{xx}[-1]|^{2}}{r_{xx}[0]}+\frac{|r_{xx}[-1]|^{2}}{r_{xx}[0]}](https://lysario.de/wp-content/cache/tex_01f37e6441a7f41cb64a59ee3f672642.png) | ||
 | ![r_{xx}[0]- \frac{|r_{xx}[-1]|^{2}}{r_{xx}[0]}](https://lysario.de/wp-content/cache/tex_9955d844fdbfc133a5d83f59c186baa2.png) | (4) |
This result can also be obtained by the equations [1, eq. 3.36, eq. 3.37]. They provide the solution for the optimal prediction parameter of a linear predictor
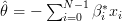 , that minimizes the MSE and the minimum MSE. Note that in the book
, that minimizes the MSE and the minimum MSE. Note that in the book 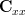 is used instead of
is used instead of 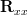 and
and 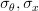 instead of
instead of ![r_{\theta \theta}[0]](https://lysario.de/wp-content/cache/tex_c0219a326d69241fe834eb6473323994.png) and
and ![r_{xx}[0]](https://lysario.de/wp-content/cache/tex_92c5630642b279858745d05d4097b3fc.png) . This is only correct for a zero mean random process
. This is only correct for a zero mean random process ![x[n]](https://lysario.de/wp-content/cache/tex_d3baaa3204e2a03ef9528a7d631a4806.png) , as it is assumed in the derivation of the formula in the book. The formula for the optimal coefficients is thus:
, as it is assumed in the derivation of the formula in the book. The formula for the optimal coefficients is thus:
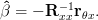 | |||
The minimum MSE is for a general signal
![x[n]](https://lysario.de/wp-content/cache/tex_d3baaa3204e2a03ef9528a7d631a4806.png) is equal to:
is equal to:
![MSE_{MIN}=r_{\theta\theta}[0]+\mathbf{r}_{\theta x}^{H}\mathbf{\hat{\beta}}.](https://lysario.de/wp-content/cache/tex_41165fdd506a9ccbe24cd309481c1259.png) | |||
Translating the formulas to the notation of the exercise, we obtain
![\theta =x[n]](https://lysario.de/wp-content/cache/tex_ebceea97dfa3ecda473bc59100754274.png) ,
,![\mathbf{x}=x[n-1]](https://lysario.de/wp-content/cache/tex_fe89bc16cb2f5f0ba3baf853dd3118a7.png) ,
, 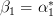 and
and ![\mathbf{r}_{\theta x}=E\left\{\mathbf{x}\theta^{H}\right\}=E\left\{x^{\ast}[n]x[n-1]\right\}=r_{xx}[-1]](https://lysario.de/wp-content/cache/tex_fea96e545397b9f1724990fedcc117e0.png) ,
, ![\mathbf{R}_{xx}=E\left\{ x^{\ast}[n-1]x[n-1]\right\}=r_{xx}[0]](https://lysario.de/wp-content/cache/tex_b0865d4540df90fe1b90e211dd8a9da5.png) and for a zero mean process
and for a zero mean process ![r_{xx}[0]=\sigma_{\theta}^{2}=\sigma_{x}^{2}](https://lysario.de/wp-content/cache/tex_23b9fa5525a8d3c398f88495687c81bb.png) .
The optimal prediction parameter
.
The optimal prediction parameter 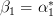 is thus given by:
is thus given by:
![\alpha_{1}=-\frac{r^{\ast}_{xx}[-1]}{r_{xx}[0]}](https://lysario.de/wp-content/cache/tex_2d9d84c2494b2f1c222f12e82cf663ee.png) | (5) | ||
while the minimum MSE is given by:
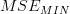 |  | ![r_{xx}[0]+r^{\ast}_{xx}[-1] \alpha^{\ast}_{1}](https://lysario.de/wp-content/cache/tex_bbf9d2e7219e49cd1a39847b87de69ba.png) | |
 | ![r_{xx}[0]- \frac{r^{\ast}_{xx}[-1] r_{xx}[-1]}{r_{xx}[0]}](https://lysario.de/wp-content/cache/tex_7d53f95f8c27d3d38ae1eb1d3d82831a.png) | ||
 | ![r_{xx}[0]- \frac{|r_{xx}[-1]|^{2}}{r_{xx}[0]}](https://lysario.de/wp-content/cache/tex_2ea2b8f4ba4178e8b5f4c358be91f161.png) | (6) |
Which is equal to the solution that was obtained using the orthogonality principle (4).
[1] Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”, Prentice Hall, ISBN: 0-13-598582-X.
Leave a reply