Lysario – by Panagiotis Chatzichrisafis
"ούτω γάρ ειδέναι το σύνθετον υπολαμβάνομεν, όταν ειδώμεν εκ τίνων και πόσων εστίν …"
Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”,p. 61 exercise 3.8
Author: Panagiotis22 Sep
In [1, p. 61 exercise 3.8] we are asked to prove that the sample mean is a sufficient statistic for the mean under the conditions of [1, p. 61 exercise 3.4].
Assuming that 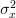 is known. We are asked to find the MLE of the mean by maximizing
is known. We are asked to find the MLE of the mean by maximizing 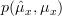 .
.
Solution: By definition [1, p. 48] a sufficient statistic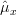 of
of 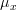 if the conditional probability density function
if the conditional probability density function 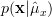 does not depend on
does not depend on 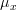 . By the Neyman-Fisher factorization theorem the statistic will be sufficient if and only if it is possible to write the PDF as:
. By the Neyman-Fisher factorization theorem the statistic will be sufficient if and only if it is possible to write the PDF as:
The joint p.d.f is given by:
Setting
and
we see at once that the equation (2) has the form of the Neyman-Fisher factorization theorem (1), thus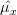 is sufficient.
The MLE of
is sufficient.
The MLE of 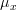 for the measurement
for the measurement 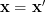 is obtained by:
is obtained by:
Thus the MLE estimator of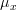 is equal to the sample mean
is equal to the sample mean 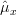 as already obtained in [2]. QED.
as already obtained in [2]. QED.
[1] Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”, Prentice Hall, ISBN: 0-13-598582-X.
[2] Chatzichrisafis: “Solution of exercise 3.7 from Kay’s Modern Spectral Estimation - Theory and Applications”.
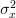 is known. We are asked to find the MLE of the mean by maximizing
is known. We are asked to find the MLE of the mean by maximizing 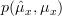 .
.
Solution: By definition [1, p. 48] a sufficient statistic
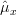 of
of 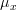 if the conditional probability density function
if the conditional probability density function 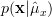 does not depend on
does not depend on 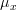 . By the Neyman-Fisher factorization theorem the statistic will be sufficient if and only if it is possible to write the PDF as:
. By the Neyman-Fisher factorization theorem the statistic will be sufficient if and only if it is possible to write the PDF as:
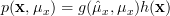 | (1) | ||
The joint p.d.f is given by:
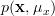 |  | 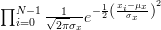 | |
 | 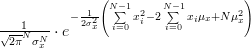 | ||
 | 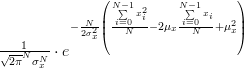 | ||
 | 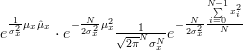 | (2) |
Setting
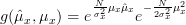 | |||
and
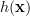 |  | 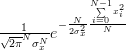 | |
 | 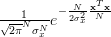 |
we see at once that the equation (2) has the form of the Neyman-Fisher factorization theorem (1), thus
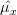 is sufficient.
The MLE of
is sufficient.
The MLE of 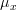 for the measurement
for the measurement 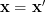 is obtained by:
is obtained by:
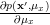 |  |  | |
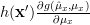 |  | 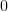 | |
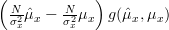 |  | 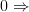 | (3) |
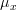 |  | 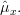 | (4) |
Thus the MLE estimator of
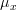 is equal to the sample mean
is equal to the sample mean 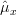 as already obtained in [2]. QED.
as already obtained in [2]. QED.[1] Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”, Prentice Hall, ISBN: 0-13-598582-X.
[2] Chatzichrisafis: “Solution of exercise 3.7 from Kay’s Modern Spectral Estimation - Theory and Applications”.
Leave a reply