Lysario – by Panagiotis Chatzichrisafis
"ούτω γάρ ειδέναι το σύνθετον υπολαμβάνομεν, όταν ειδώμεν εκ τίνων και πόσων εστίν …"
Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”,p. 34 exercise 2.3
Author: Panagiotis27 Sep
In exercise [1, p. 34 exercise 2.3] we are asked to prove that the normalized DFT matrix given in [1, p. 21, (2.22)] is unitary.
Solution: The normalized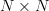 DFT matrix is given by:
DFT matrix is given by:
The above multiplication results in:
The elements of the matrix![\mathbf{W}\mathbf{W}^H=[w_{ml}]](https://lysario.de/wp-content/cache/tex_a035d0fb4b0914b3af9e2504933a3ac5.png) for
for 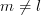 are sums of geometric series which are given by [2, p. 16]
are sums of geometric series which are given by [2, p. 16] 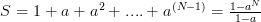 .
Thus e.g. for
.
Thus e.g. for 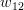 the following result is derived:
the following result is derived:
Similar the other terms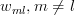 of the matrix are also equal to zero and therefore
of the matrix are also equal to zero and therefore 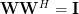 , where
, where 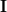 is the identity matrix. Thus the normalized DFT matrix is unitary. QED.
is the identity matrix. Thus the normalized DFT matrix is unitary. QED.
[1] Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”, Prentice Hall, ISBN: 0-13-598582-X.
[2] Bronstein and Semdjajew and Musiol and Muehlig: “Taschenbuch der Mathematik”, Verlag Harri Deutsch Thun und Frankfurt am Main, ISBN: 3-8171-2003-6.
Solution: The normalized
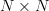 DFT matrix is given by:
DFT matrix is given by:
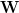 |  | ![\frac{1}{{\sqrt N }}\left[ {\begin{array}{*{20}c}
1 & 1 & \cdots & 1 \\
1 & {e^{( - j\frac{{2\pi }}{N})} } & \cdots & {e^{( - j\frac{{2\pi }}{N} \cdot (N - 1))} } \\
1 & {e^{( - j\frac{{2\pi }}{N} \cdot 2)} } & \cdots & {e^{( - j\frac{{2\pi }}{N} \cdot 2 \cdot (N - 1))} } \\
\vdots & \vdots & \vdots & \vdots \\
1 & {e^{( - j\frac{{2\pi }}{N} \cdot (N - 1))} } & \cdots & {e^{( - j\frac{{2\pi }}{N} \cdot (N - 1)^2 )} } \\
\end{array}} \right]](https://lysario.de/wp-content/cache/tex_db17e32f3812c087e4bebf581f273b43.png) | (1) |
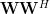 |  | ![\frac{1}{N}\left[ {\begin{array}{*{20}c}
1 & 1 & \cdots & 1 \\
1 & {e^{( - j\frac{{2\pi }}{N})} } & \cdots & {e^{( - j\frac{{2\pi }}{N} \cdot (N - 1))} } \\
1 & {e^{( - j\frac{{2\pi }}{N} \cdot 2)} } & \cdots & {e^{( - j\frac{{2\pi }}{N} \cdot 2 \cdot (N - 1))} } \\
\vdots & \vdots & \vdots & \vdots \\
1 & {e^{( - j\frac{{2\pi }}{N} \cdot (N - 1))} } & \cdots & {e^{( - j\frac{{2\pi }}{N} \cdot (N - 1)^2 )} } \\
\end{array}} \right]](https://lysario.de/wp-content/cache/tex_a88d1c54ff97c730d80824cfdb576239.png) |
![\cdot \left[ {\begin{array}{*{20}c}
1 & 1 & \cdots & 1 \\
1 & {e^{(j\frac{{2\pi }}{N})} } & \cdots & {e^{(j\frac{{2\pi }}{N} \cdot (N - 1))} } \\
1 & {e^{(j\frac{{2\pi }}{N} \cdot 2)} } & \cdots & {e^{(j\frac{{2\pi }}{N} \cdot 2 \cdot (N - 1))} } \\
\vdots & \vdots & \vdots & \vdots \\
1 & {e^{(j\frac{{2\pi }}{N} \cdot (N - 1))} } & \cdots & {e^{(j\frac{{2\pi }}{N} \cdot (N - 1)^2 )} } \\
\end{array}} \right]](https://lysario.de/wp-content/cache/tex_146649186246d8d8de23f55daf459063.png) | (2) | ||
The above multiplication results in:
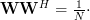 | |||
![\cdot \left[ {\begin{array}{*{20}c}
N & {\sum\limits_{k = 0}^{N - 1} {e^{(j\frac{{2\pi }}{N}k)} } } & \cdots & {\sum\limits_{k = 0}^{N - 1} {e^{(j\frac{{2\pi }}{N} \cdot (N - 1) \cdot k)} } } \\
{\sum\limits_{k = 0}^{N - 1} {e^{ - (j\frac{{2\pi }}{N}k)} } } & N & \cdots & {\sum\limits_{k = 0}^{N - 1} {e^{(j\frac{{2\pi }}{N} \cdot (N - 2) \cdot k)} } } \\
{\sum\limits_{k = 0}^{N - 1} {e^{ - (j\frac{{2\pi }}{N} \cdot 2 \cdot k)} } } & {\sum\limits_{k = 0}^{N - 1} {e^{ - (j\frac{{2\pi }}{N}k)} } } & \cdots & {\sum\limits_{k = 0}^{N - 1} {e^{(j\frac{{2\pi }}{N} \cdot (N - 3) \cdot k)} } } \\
\vdots & \vdots & \vdots & \vdots \\
{\sum\limits_{k = 0}^{N - 1} {e^{ - (j\frac{{2\pi }}{N} \cdot (N - 1) \cdot k)} } } & {\sum\limits_{k = 0}^{N - 1} {e^{ - (j\frac{{2\pi }}{N} \cdot N \cdot k)} } } & \cdots & N \\
\end{array}} \right]](https://lysario.de/wp-content/cache/tex_5a65450cbde6732d744be25b39a890da.png) | (3) | ||
The elements of the matrix
![\mathbf{W}\mathbf{W}^H=[w_{ml}]](https://lysario.de/wp-content/cache/tex_a035d0fb4b0914b3af9e2504933a3ac5.png) for
for 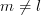 are sums of geometric series which are given by [2, p. 16]
are sums of geometric series which are given by [2, p. 16] 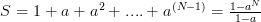 .
Thus e.g. for
.
Thus e.g. for 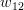 the following result is derived:
the following result is derived:
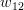 |  | 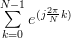 | |
 | 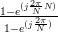 | ||
 |  | ||
Similar the other terms
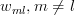 of the matrix are also equal to zero and therefore
of the matrix are also equal to zero and therefore 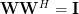 , where
, where 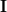 is the identity matrix. Thus the normalized DFT matrix is unitary. QED.
is the identity matrix. Thus the normalized DFT matrix is unitary. QED. [1] Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”, Prentice Hall, ISBN: 0-13-598582-X.
[2] Bronstein and Semdjajew and Musiol and Muehlig: “Taschenbuch der Mathematik”, Verlag Harri Deutsch Thun und Frankfurt am Main, ISBN: 3-8171-2003-6.
Leave a reply