Lysario – by Panagiotis Chatzichrisafis
"ούτω γάρ ειδέναι το σύνθετον υπολαμβάνομεν, όταν ειδώμεν εκ τίνων και πόσων εστίν …"
Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”,p. 34 exercise 2.8
Author: Panagiotis22 Dez
In exercise [1, p. 34 exercise 2.8] we are asked to find the inverse of the 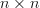 hermitian matrix
hermitian matrix  given by [1, (2.27)] by recursively applying Woodbury’s identity. This should be done by considering the cases where
given by [1, (2.27)] by recursively applying Woodbury’s identity. This should be done by considering the cases where 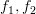 are arbitrary and where
are arbitrary and where 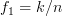 ,
, 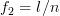 for
for 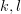 beeing distinct integers in the range
beeing distinct integers in the range ![\left[ -n/2,n/2-1 \right]](https://lysario.de/wp-content/cache/tex_349760367e158b72823c089231e45245.png) for
for  even and
even and ![\left[ -(n-1)/2,(n-1)/2 \right]](https://lysario.de/wp-content/cache/tex_bbbbf77ffaa65be463cde297b83e452b.png) for
for  odd.
odd.
Solution: Woodbury’s identity is given by [1, p. 24, (2.32)]:
The matrix given by [1, (2.27)] is
Let
then the marix may be rewritten as:
may be rewritten as:
Applying the relation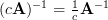 and Woodbury’s identity to (4) yields:
and Woodbury’s identity to (4) yields:
But the inverse of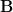 in (5) can be obtained from (3) by applying once more Woodbury’s identity:
in (5) can be obtained from (3) by applying once more Woodbury’s identity:
The previous equation is obtained by utilizing the relation
Note further that the vectors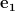 and
and 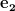 are normal:
are normal:
as the sum (8) is a geometric series [2, p. 16]. In order to obtain a simplified result for the inverse of the matrix we have to compute also the matrix products of
we have to compute also the matrix products of 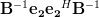 and
and 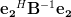 .
Utilizing the fact that the vectors
.
Utilizing the fact that the vectors 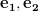 are normal (9) and using the inverse of the matrix
are normal (9) and using the inverse of the matrix 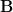 which is provided by (6) we obtain the following relations:
which is provided by (6) we obtain the following relations:
As also:
Thus
and because of (7) we also can simplify
Using (6) and the last two relations (10),(11) the inverse of the matrix (5) can be simplified to:
(5) can be simplified to:
which is the inverse of the matrix obtained by recursively applying Woodbury’s identity.
obtained by recursively applying Woodbury’s identity.
[1] Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”, Prentice Hall, ISBN: 0-13-598582-X.
[2] Bronstein and Semdjajew and Musiol and Muehlig: “Taschenbuch der Mathematik”, Verlag Harri Deutsch Thun und Frankfurt am Main, ISBN: 3-8171-2003-6.
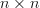 hermitian matrix
hermitian matrix  given by [1, (2.27)] by recursively applying Woodbury’s identity. This should be done by considering the cases where
given by [1, (2.27)] by recursively applying Woodbury’s identity. This should be done by considering the cases where 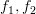 are arbitrary and where
are arbitrary and where 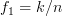 ,
, 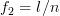 for
for 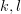 beeing distinct integers in the range
beeing distinct integers in the range ![\left[ -n/2,n/2-1 \right]](https://lysario.de/wp-content/cache/tex_349760367e158b72823c089231e45245.png) for
for  even and
even and ![\left[ -(n-1)/2,(n-1)/2 \right]](https://lysario.de/wp-content/cache/tex_bbbbf77ffaa65be463cde297b83e452b.png) for
for  odd.
odd.
Solution: Woodbury’s identity is given by [1, p. 24, (2.32)]:
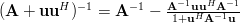 | (1) | ||
The matrix given by [1, (2.27)] is
 |  | 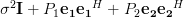 | (2) |
 | ![P_2\left[ \left( \frac{\sigma^2}{P_2} \mathbf{I}+\frac{P_1}{P_2}\mathbf{e_1}\mathbf{e_1}^H \right)+ \mathbf{e_2}\mathbf{e_2}^H \right]](https://lysario.de/wp-content/cache/tex_0a900bb79cc9f01e6a9fbaca9753ad97.png) | ||
 | ![P_2\left[ \frac{P_1}{P_2} \left( \frac{\sigma^2}{P_1} \mathbf{I}+\mathbf{e_1}\mathbf{e_1}^H \right)+ \mathbf{e_2}\mathbf{e_2}^H \right]](https://lysario.de/wp-content/cache/tex_2f4ec9c1ea92cfe1cd49bf0f55cb03be.png) |
Let
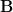 |  | 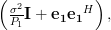 | (3) |
then the marix
 may be rewritten as:
may be rewritten as:
 |  | ![P_2\left[ \frac{P_1}{P_2} \mathbf{B}+ \mathbf{e_2}\mathbf{e_2}^H \right].](https://lysario.de/wp-content/cache/tex_1e7c62444f7a085a557f1276edd8682f.png) | (4) |
Applying the relation
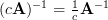 and Woodbury’s identity to (4) yields:
and Woodbury’s identity to (4) yields:
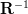 |  | ![\frac{1}{P_2}\left[\frac{P_2}{P_1}\mathbf{B}^{-1}-\frac{(\frac{P_2}{P_1})^{2}\mathbf{B}^{-1}\mathbf{e_2}\mathbf{e_2}^H \mathbf{B}^{-1}}{1+\frac{P_2}{P_1} \mathbf{e_2}^H\mathbf{B}^{-1}\mathbf{e_2}} \right]](https://lysario.de/wp-content/cache/tex_62a23596fe1e6a169eecffbb9d4d18f1.png) | (5) |
But the inverse of
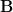 in (5) can be obtained from (3) by applying once more Woodbury’s identity:
in (5) can be obtained from (3) by applying once more Woodbury’s identity:
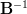 |  | 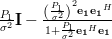 | |
 | 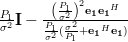 | ||
 | 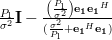 | ||
 | 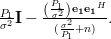 | (6) |
The previous equation is obtained by utilizing the relation
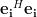 |  | ![\left[ {\begin{array}{*{20}c}
1 & {e^{-j2\pi f_i } } & \cdots & {e^{-j2\pi (n - 1)f_i } }
\end{array}} \right] \left[ {\begin{array}{*{20}c}
1 \\
{e^{j2\pi f_i } } \\
\vdots \\
{e^{j2\pi (n - 1)f_i } } \\
\end{array}} \right]](https://lysario.de/wp-content/cache/tex_3a6f3857cccd288278be800413c9131b.png) | |
 | 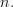 | (7) |
Note further that the vectors
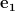 and
and 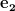 are normal:
are normal:
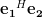 |  | ![\left[ {\begin{array}{*{20}c}
1 & {e^{-j2\pi f_1 } } & \cdots & {e^{-j2\pi (n - 1)f_1 } }
\end{array}} \right] \left[ {\begin{array}{*{20}c}
1 \\
{e^{j2\pi f_2 } } \\
\vdots \\
{e^{j2\pi (n - 1)f_2 } } \\
\end{array}} \right]](https://lysario.de/wp-content/cache/tex_f9cdeb9889c6ed8a5f405ed5672d35ca.png) | |
 | 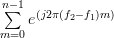 | (8) | |
 | 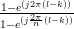 | ||
 | 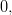 | (9) |
as the sum (8) is a geometric series [2, p. 16]. In order to obtain a simplified result for the inverse of the matrix
 we have to compute also the matrix products of
we have to compute also the matrix products of 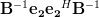 and
and 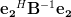 .
Utilizing the fact that the vectors
.
Utilizing the fact that the vectors 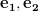 are normal (9) and using the inverse of the matrix
are normal (9) and using the inverse of the matrix 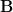 which is provided by (6) we obtain the following relations:
which is provided by (6) we obtain the following relations:
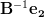 |  | 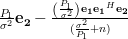 | |
 | 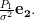 |
As also:
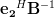 |  | 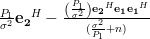 | |
 | 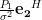 |
Thus
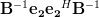 |  | 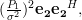 | (10) |
and because of (7) we also can simplify
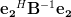 |  | 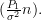 | (11) |
Using (6) and the last two relations (10),(11) the inverse of the matrix
 (5) can be simplified to:
(5) can be simplified to:
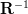 |  | ![\frac{1}{P_2}\left[\frac{P_2}{P_1} \left(\frac{P_1}{\sigma^2}\mathbf{I}-\frac{\left(\frac{P_1}{\sigma^2}\right)\mathbf{e_1}\mathbf{e_1}^H}{(\frac{\sigma^2}{P_1}+n)} \right)-\frac{(\frac{P_2}{P_1})^{2}(\frac{P_1}{\sigma^2})^2 \mathbf{e_2}\mathbf{e_2}^H}{1+\frac{P_2}{P_1} (\frac{P_1}{\sigma^2})n} \right]](https://lysario.de/wp-content/cache/tex_c3c3d4e859887952583b7a8a277ee6af.png) | |
 | 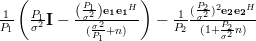 | ||
 | 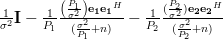 | ||
 | 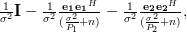 |
which is the inverse of the matrix
 obtained by recursively applying Woodbury’s identity.
obtained by recursively applying Woodbury’s identity. [1] Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”, Prentice Hall, ISBN: 0-13-598582-X.
[2] Bronstein and Semdjajew and Musiol and Muehlig: “Taschenbuch der Mathematik”, Verlag Harri Deutsch Thun und Frankfurt am Main, ISBN: 3-8171-2003-6.
Leave a reply