Lysario – by Panagiotis Chatzichrisafis
"ούτω γάρ ειδέναι το σύνθετον υπολαμβάνομεν, όταν ειδώμεν εκ τίνων και πόσων εστίν …"
Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”,p. 62 exercise 3.19
Author: Panagiotis17 Mai
In [1, p. 62 exercise 3.19] we are asked to find for the multiple sinusoidal process
the ensemble ACF and the temporal ACF as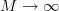 , where the
, where the 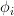 ‘s are all uniformly distributed random variables on
‘s are all uniformly distributed random variables on 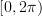 and independent of each other. We are also asked to determine if this random process is autocorrelation ergodic.
and independent of each other. We are also asked to determine if this random process is autocorrelation ergodic.
Solution: We note that the joint p.d.f of the uniformly random variables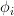 is given by
is given by 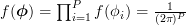 , with domain
, with domain 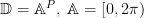 we can proceed to calculate the ensemble autocorrelation function which is defined as:
we can proceed to calculate the ensemble autocorrelation function which is defined as:
As in exercise [2] we can use the trigonometric relation [3, p. 810] :
(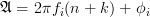 ,
, 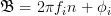 ) to further simplify the expression for the ensemble autocorrelation function:
) to further simplify the expression for the ensemble autocorrelation function:
Having obtained the ensemble autocorrelation function we can proceed to obtain the temporal autocorrelation function, which we hope will be a good approximation![\hat{r}_{xx}[k]](https://lysario.de/wp-content/cache/tex_ca6151c7d846302aeb171d16bcaf24ce.png) to the ensemble autocorrelation function
to the ensemble autocorrelation function ![r_{xx}[k]](https://lysario.de/wp-content/cache/tex_86d1714abfafbac31f80e60727d3add6.png) . By definition the temporal autocorrelation function is given by
. By definition the temporal autocorrelation function is given by
The second sum of the previous relation can be simplified by one of the derived formulas of [2], for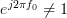 :
:
Thus the temporal autocorrelation function may be expressed, as long as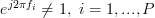 as:
as:
In order to simplify the relation further, especially the first sum, we will again use (1), with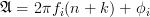 and
and 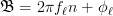 , and thus :
, and thus :
We see that both distinct parts are of the form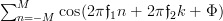 , and thus it remains to simplify this relation. Again using a trigonometric formula [3, p. 810]:
, and thus it remains to simplify this relation. Again using a trigonometric formula [3, p. 810]:
with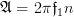 and
and 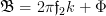 we can simplify the relation as:
we can simplify the relation as:
Furthermore it was shown in [2] that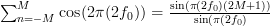 , for
, for 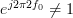 , so we can further simplify the previous relation by:
, so we can further simplify the previous relation by:
Thus finally we can simplify (5) by:
So finally the temporal autocorrelation (4) can be reduced using (8) to the following formula:
Rearranging the terms on the right we see that the temporal autocorrelation function equals the ensemble autocorrelation function with an additional error , which we have derived for the the case when
, which we have derived for the the case when 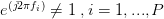 :
:
At once we see again that when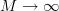 that the error goes to zero
that the error goes to zero 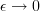 . Thus the random process of the sum of sinusoids is also autocorrelation ergodic as long as
. Thus the random process of the sum of sinusoids is also autocorrelation ergodic as long as 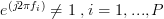 . It is also easy to recognize, by using the argumentation of the previous exercise [2] , that this is not true if
. It is also easy to recognize, by using the argumentation of the previous exercise [2] , that this is not true if 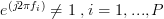 does not hold. In this case parts of the the error of equation (3) are proportional to
does not hold. In this case parts of the the error of equation (3) are proportional to 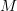 as was already observed in [2] . QED.
as was already observed in [2] . QED.
[1] Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”, Prentice Hall, ISBN: 0-13-598582-X.
[2] Chatzichrisafis: “Solution of exercise 3.18 from Kay’s Modern Spectral Estimation - Theory and Applications”.
[3] Granino A. Korn and Theresa M. Korn: “Mathematical Handbook for Scientists and Engineers”, Dover, ISBN: 978-0-486-41147-7.
![x[n]=\sum\limits_{i=1}^{P}A_{i}\cos(2\pi f_{i}n+\phi_{i})](https://lysario.de/wp-content/cache/tex_18c06f6747166204af88405a37dafba0.png) | |||
the ensemble ACF and the temporal ACF as
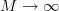 , where the
, where the 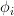 ‘s are all uniformly distributed random variables on
‘s are all uniformly distributed random variables on 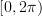 and independent of each other. We are also asked to determine if this random process is autocorrelation ergodic.
and independent of each other. We are also asked to determine if this random process is autocorrelation ergodic.
Solution: We note that the joint p.d.f of the uniformly random variables
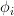 is given by
is given by 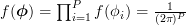 , with domain
, with domain 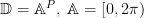 we can proceed to calculate the ensemble autocorrelation function which is defined as:
we can proceed to calculate the ensemble autocorrelation function which is defined as:
![r_{xx}[k]](https://lysario.de/wp-content/cache/tex_86d1714abfafbac31f80e60727d3add6.png) |  | ![E \left\{ x^{\star}[n] x[n+k] \right\}](https://lysario.de/wp-content/cache/tex_ed33a5bfeea3e43bd2105939d30e1f9e.png) | |
 | 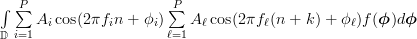 | ||
 | 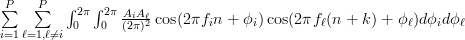 | ||
 | 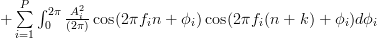 | ||
 | ![\sum\limits_{i=1}^{P} \sum\limits_{\ell=1, \ell\neq i}^{P} \int_{0}^{2\pi} \frac{A_{i}A_{\ell}}{(2\pi)^{2}} \underbrace{\left[ \sin(2\pi f_{i}n+\phi_{i})\right]_{0}^{2\pi}}_{=0}\cos(2\pi f_{\ell}(n+k)+\phi_{\ell}) d\phi_{\ell}](https://lysario.de/wp-content/cache/tex_f59990cd0ecc01009a055fee0e76d657.png) | ||
 | 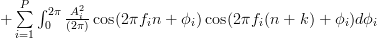 | ||
 |  |
As in exercise [2] we can use the trigonometric relation [3, p. 810] :
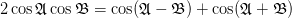 | (1) | ||
(
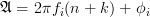 ,
, 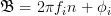 ) to further simplify the expression for the ensemble autocorrelation function:
) to further simplify the expression for the ensemble autocorrelation function:
![r_{xx}[k]](https://lysario.de/wp-content/cache/tex_86d1714abfafbac31f80e60727d3add6.png) |  | 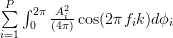 | |
 | 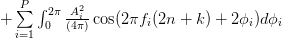 | ||
 | 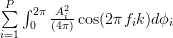 | ||
 | ![+\sum\limits_{i=1}^{P} \frac{A_{i}^{2}}{(8\pi)}\underbrace{\left[\sin(2\pi f_{i}(2n+k)+2 \phi_{i})\right]_{\phi_{i}=0}^{2\pi}}_{=0}](https://lysario.de/wp-content/cache/tex_e0f28f57d09e6a6c6e1d976a8fbfe1c0.png) | ||
 | 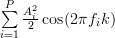 | (2) |
Having obtained the ensemble autocorrelation function we can proceed to obtain the temporal autocorrelation function, which we hope will be a good approximation
![\hat{r}_{xx}[k]](https://lysario.de/wp-content/cache/tex_ca6151c7d846302aeb171d16bcaf24ce.png) to the ensemble autocorrelation function
to the ensemble autocorrelation function ![r_{xx}[k]](https://lysario.de/wp-content/cache/tex_86d1714abfafbac31f80e60727d3add6.png) . By definition the temporal autocorrelation function is given by
. By definition the temporal autocorrelation function is given by
![\hat{r}_{xx}[k]](https://lysario.de/wp-content/cache/tex_ca6151c7d846302aeb171d16bcaf24ce.png) |  | ![\frac{1}{2M+1} \sum\limits_{n=-M}^{M} x[n+k]x^{\star}[n]](https://lysario.de/wp-content/cache/tex_7a001667ad6d1295e121ad3d94ee3ca1.png) | |
 | 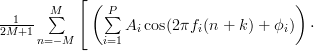 | ||
 | ![\cdot \left(\sum\limits_{\ell=1}^{P}A_{\ell}\cos(2\pi f_{\ell}n+\phi_{\ell}) \right)\Bigg]](https://lysario.de/wp-content/cache/tex_cd7b099c92313c3d503a8da21822744b.png) | ||
 | 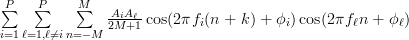 | ||
 |  | (3) |
The second sum of the previous relation can be simplified by one of the derived formulas of [2], for
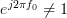 :
:
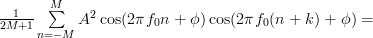 | |||
 | |||
Thus the temporal autocorrelation function may be expressed, as long as
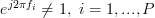 as:
as:
![\hat{r}_{xx}[k]](https://lysario.de/wp-content/cache/tex_ca6151c7d846302aeb171d16bcaf24ce.png) |  | 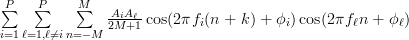 | |
 |  | ||
 | 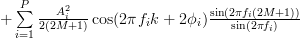 | (4) |
In order to simplify the relation further, especially the first sum, we will again use (1), with
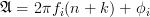 and
and 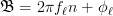 , and thus :
, and thus :
 | 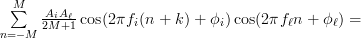 | ||
 |  | ||
 | 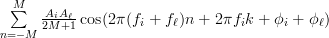 | (5) |
We see that both distinct parts are of the form
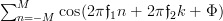 , and thus it remains to simplify this relation. Again using a trigonometric formula [3, p. 810]:
, and thus it remains to simplify this relation. Again using a trigonometric formula [3, p. 810]:
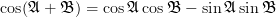 | (6) | ||
with
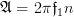 and
and 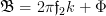 we can simplify the relation as:
we can simplify the relation as:
 | |||
 | 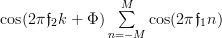 | ||
 | 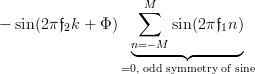 | ||
 | 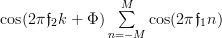 | ||
Furthermore it was shown in [2] that
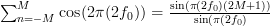 , for
, for 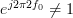 , so we can further simplify the previous relation by:
, so we can further simplify the previous relation by:
 | |||
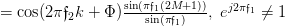 | (7) | ||
Thus finally we can simplify (5) by:
 | 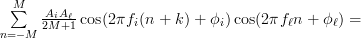 | ||
 | 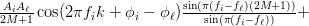 | ||
 | 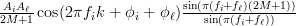 | (8) |
So finally the temporal autocorrelation (4) can be reduced using (8) to the following formula:
![\hat{r}_{xx}[k]](https://lysario.de/wp-content/cache/tex_ca6151c7d846302aeb171d16bcaf24ce.png) |  | 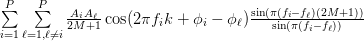 | |
 | 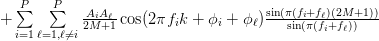 | ||
 |  | ||
 | 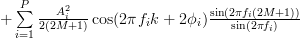 | (9) |
Rearranging the terms on the right we see that the temporal autocorrelation function equals the ensemble autocorrelation function with an additional error
 , which we have derived for the the case when
, which we have derived for the the case when 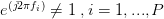 :
:
![\hat{r}_{xx}[k]](https://lysario.de/wp-content/cache/tex_ca6151c7d846302aeb171d16bcaf24ce.png) |  | 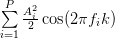 | |
 | 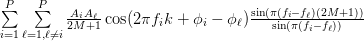 | ||
 | 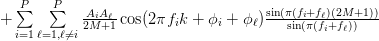 | ||
 | 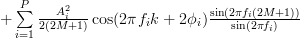 | ||
 | ![r_{xx}[k] +\epsilon](https://lysario.de/wp-content/cache/tex_31d6c64643fcd1591c423ab479644174.png) |
At once we see again that when
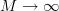 that the error goes to zero
that the error goes to zero 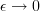 . Thus the random process of the sum of sinusoids is also autocorrelation ergodic as long as
. Thus the random process of the sum of sinusoids is also autocorrelation ergodic as long as 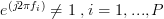 . It is also easy to recognize, by using the argumentation of the previous exercise [2] , that this is not true if
. It is also easy to recognize, by using the argumentation of the previous exercise [2] , that this is not true if 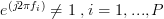 does not hold. In this case parts of the the error of equation (3) are proportional to
does not hold. In this case parts of the the error of equation (3) are proportional to 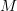 as was already observed in [2] . QED.
as was already observed in [2] . QED.[1] Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”, Prentice Hall, ISBN: 0-13-598582-X.
[2] Chatzichrisafis: “Solution of exercise 3.18 from Kay’s Modern Spectral Estimation - Theory and Applications”.
[3] Granino A. Korn and Theresa M. Korn: “Mathematical Handbook for Scientists and Engineers”, Dover, ISBN: 978-0-486-41147-7.
Leave a reply