Lysario – by Panagiotis Chatzichrisafis
"ούτω γάρ ειδέναι το σύνθετον υπολαμβάνομεν, όταν ειδώμεν εκ τίνων και πόσων εστίν …"
Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”,p. 94 exercise 4.1
Author: Panagiotis1 Feb
In problem [1, p. 94 exercise 4.1] we will show that the periodogram is an inconsistent estimator by examining the estimator at 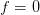 , or
, or
If![x[n]](https://lysario.de/wp-content/cache/tex_d3baaa3204e2a03ef9528a7d631a4806.png) is real white Gaussian noise process with PSD
is real white Gaussian noise process with PSD
we are asked to find the mean an variance of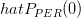 . We are asked if the variance converge to zero as
. We are asked if the variance converge to zero as 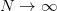 . The hint provided within the exercise is to note that
. The hint provided within the exercise is to note that
where the quantiiy inside the parenthesis is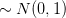 Solution:
Because
Solution:
Because ![Y = \sum_{n=0}^{N-1}\frac{x[n]}{\sigma_{x}\sqrt{N}}](https://lysario.de/wp-content/cache/tex_3dd5e12134e10cee884cdc9f326c4244.png) is distributed according to a normal distribution
is distributed according to a normal distribution 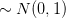 the squared variable
the squared variable 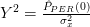 is distributed according to a
is distributed according to a 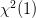 with mean
with mean 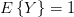 and variance
and variance 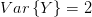 . From the previous relations we obtain the mean and the variance of the periodogram
. From the previous relations we obtain the mean and the variance of the periodogram 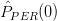 as
as
We see that while the mean converges to the true power spectral density, the variance does not converge to zero. Thus the estimator is inconsistent. QED.
[1] Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”, Prentice Hall, ISBN: 0-13-598582-X.
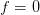 , or
, or
![\hat{P}_{PER}(0)=\frac{1}{N}\left(\sum\limits_{n=0}^{N-1}x[n]\right)^{2}.](https://lysario.de/wp-content/cache/tex_938765f09480f77020c3aad219444ca0.png) | (1) | ||
If
![x[n]](https://lysario.de/wp-content/cache/tex_d3baaa3204e2a03ef9528a7d631a4806.png) is real white Gaussian noise process with PSD
is real white Gaussian noise process with PSD
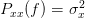 | (2) | ||
we are asked to find the mean an variance of
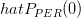 . We are asked if the variance converge to zero as
. We are asked if the variance converge to zero as 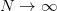 . The hint provided within the exercise is to note that
. The hint provided within the exercise is to note that
![\hat{P}_{PER}(0)= \sigma_{x}^{2} \left(\sum\limits_{n=0}^{N-1}\frac{x[n]}{\sigma_{x}\sqrt{N}}\right)^{2}](https://lysario.de/wp-content/cache/tex_df83a5d6a6944d47bfd3d103cb81d6c4.png) | (3) | ||
where the quantiiy inside the parenthesis is
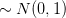 Solution:
Because
Solution:
Because ![Y = \sum_{n=0}^{N-1}\frac{x[n]}{\sigma_{x}\sqrt{N}}](https://lysario.de/wp-content/cache/tex_3dd5e12134e10cee884cdc9f326c4244.png) is distributed according to a normal distribution
is distributed according to a normal distribution 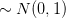 the squared variable
the squared variable 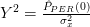 is distributed according to a
is distributed according to a 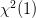 with mean
with mean 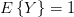 and variance
and variance 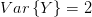 . From the previous relations we obtain the mean and the variance of the periodogram
. From the previous relations we obtain the mean and the variance of the periodogram 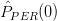 as
as
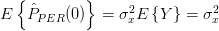 | |||
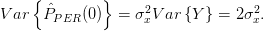 | |||
We see that while the mean converges to the true power spectral density, the variance does not converge to zero. Thus the estimator is inconsistent. QED.
[1] Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”, Prentice Hall, ISBN: 0-13-598582-X.
Leave a reply