Lysario – by Panagiotis Chatzichrisafis
"ούτω γάρ ειδέναι το σύνθετον υπολαμβάνομεν, όταν ειδώμεν εκ τίνων και πόσων εστίν …"
Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”,p. 35 exercise 2.15
Author: Panagiotis25 Jun
In [1, p. 35 exercise 2.15] we are asked to verify the formulas given for the gradient of a quadratic and linear form [1, p. 31 (2.61)].
The corresponding formulas are
and
where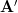 is a symmetric
is a symmetric 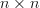 matrix with elements
matrix with elements 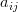 and
and 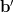 is a real
is a real 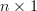 vector with elements
vector with elements 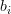 and
and 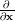 denotes the gradient of a real function in respect to
denotes the gradient of a real function in respect to
 .
.
Solution: Let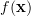 be the scalar function of the vector variable
be the scalar function of the vector variable  defined by:
defined by:
In order to identify the factors to the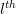 vector component of
vector component of  ,
, 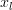 and its powers, we can rewrite the previous equation as:
and its powers, we can rewrite the previous equation as:
The first derivative of (3) in respect to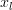 is given by:
is given by:
and replacing the dummy indexes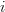 and
and 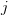 of the two sums by
of the two sums by 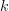 we obtain by considering the fact that the matrix is symmetric
we obtain by considering the fact that the matrix is symmetric 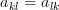 the following relation:
the following relation:
Let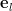 be the unit vector along the component
be the unit vector along the component 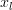 then the gradient of the matrix
then the gradient of the matrix
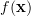 can be written as:
can be written as:
which proves the first of the formulas [1, p. 31 (2.61)]. In order to prove the second formula we proceed in a similar way by defining the scalar function
Thus the derivative in respect to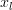 is simply:
is simply:
and the gradient is given by
The last equation proves the second relation of the formulas [1, p. 31 (2.61)]. QED.
[1] Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”, Prentice Hall, ISBN: 0-13-598582-X.
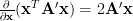 | (1) | ||
and
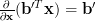 | (2) | ||
where
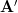 is a symmetric
is a symmetric 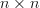 matrix with elements
matrix with elements 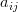 and
and 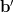 is a real
is a real 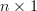 vector with elements
vector with elements 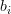 and
and 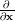 denotes the gradient of a real function in respect to
denotes the gradient of a real function in respect to
 .
.
Solution: Let
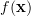 be the scalar function of the vector variable
be the scalar function of the vector variable  defined by:
defined by:
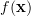 |  | 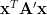 | |
 | 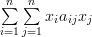 | ||
 | 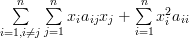 |
In order to identify the factors to the
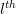 vector component of
vector component of  ,
, 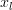 and its powers, we can rewrite the previous equation as:
and its powers, we can rewrite the previous equation as:
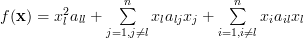 | |||
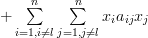 | (3) | ||
The first derivative of (3) in respect to
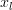 is given by:
is given by:
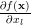 |  | 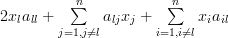 | (4) |
and replacing the dummy indexes
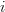 and
and 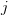 of the two sums by
of the two sums by 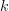 we obtain by considering the fact that the matrix is symmetric
we obtain by considering the fact that the matrix is symmetric 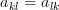 the following relation:
the following relation:
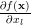 |  | 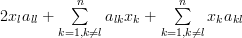 | |
 | 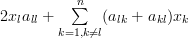 | ||
 | 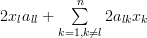 | ||
 | 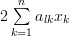 |
Let
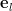 be the unit vector along the component
be the unit vector along the component 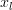 then the gradient of the matrix
then the gradient of the matrix
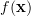 can be written as:
can be written as:
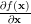 |  | 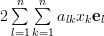 | |
 | 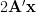 | (5) |
which proves the first of the formulas [1, p. 31 (2.61)]. In order to prove the second formula we proceed in a similar way by defining the scalar function
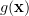 |  | 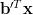 | |
 | 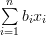 | (6) |
Thus the derivative in respect to
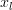 is simply:
is simply:
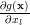 |  | 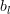 |
and the gradient is given by
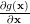 |  | 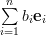 | |
 | 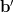 |
The last equation proves the second relation of the formulas [1, p. 31 (2.61)]. QED.
[1] Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”, Prentice Hall, ISBN: 0-13-598582-X.
One Response for "Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”,p. 35 exercise 2.15"
[...] of the gradient of a quadratic form of a real matrix which is not symmetric. We reproduce from [2, relation (4) from the solution of exercise 2.15] the formula for the real matrix and the real vector [...]
Leave a reply