Lysario – by Panagiotis Chatzichrisafis
"ούτω γάρ ειδέναι το σύνθετον υπολαμβάνομεν, όταν ειδώμεν εκ τίνων και πόσων εστίν …"
Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”,p. 34 exercise 2.12
Author: Panagiotis1 Apr
In [1, p. 34 exercise 2.12] we are asked to verify the equations given for the Cholesky decomposition, [1, (2.53)-(2.55)]. Furthermore it is requested to use these equations to find the inverse of the matrix given in problem [1, 2.7].
Solution: The Cholesky decomposition provides a numeric approach for solving linear equations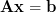 . First the matrix
. First the matrix 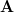 is decomposed
as a matrix product
is decomposed
as a matrix product 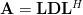 , where
, where 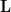 is a lower triangular matrix with the elements on the main diagonal beeing ones
is a lower triangular matrix with the elements on the main diagonal beeing ones 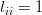 , and
, and 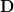 a diagonal matrix. In order to verify [1, (2.53)] we set
a diagonal matrix. In order to verify [1, (2.53)] we set 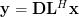 or
or
which is written analytically as:
In order to obtain the solution for the vector the previous set of equations can be rewritten as
the previous set of equations can be rewritten as
The last equations verify [1, (2.53)]. We had previously set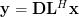 from which we can derive
the equation
from which we can derive
the equation 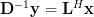 . Again expanding the previous compact matrix notation the following set of equations can be obtained:
. Again expanding the previous compact matrix notation the following set of equations can be obtained:
The solution for the vector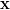 can be found by rewriting the previous set of equations:
can be found by rewriting the previous set of equations:
The set of equations (2,3) verify [1, (2.54)]. Equation [1, (2.55)] has still to be verified. This equation provides the algorithm to decompose the matrix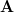 . Let
. Let ![\mathbf{L}=[l_{ij}]](https://lysario.de/wp-content/cache/tex_438a67ce1c3c41c2f40f2f5c6d46ec6e.png) with
with
Thus
Furthermore let![\mathbf{D}=[d_{ij}]](https://lysario.de/wp-content/cache/tex_f8de7c8a00fbe8abeae4be76ac36c583.png) with
with
The elements of the matrix product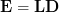 are given by
are given by
and the elements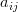 of
of 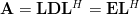 are obtained by
are obtained by 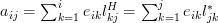 (because
(because 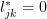 for
for 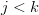 ).
When the elements
).
When the elements 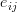 are replaced by the corresponding sum (8) then the elements
are replaced by the corresponding sum (8) then the elements 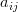 can be further expanded to:
can be further expanded to:
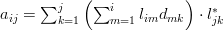 . But
. But 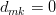 , for
, for 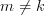 and thus:
and thus:
The last equation (9) is a consequence of the fact that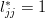 . A recursive formula for
. A recursive formula for 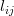 can be derived when
can be derived when 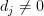 :
:
Equation (10) can be identified as the second part of the relation [1, (2.55)]. The first part is obtained by simply setting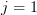 . In this case the second summand degenerates and the relation can be written as:
. In this case the second summand degenerates and the relation can be written as: 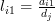 .
From (9) by setting
.
From (9) by setting 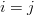 the following relation emerges:
the following relation emerges:
and again for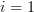 the second summand degenerates and we obtain the relation
the second summand degenerates and we obtain the relation 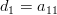 .
In order to find the inverse of the real matrix given in problem [1, 2.7]:
.
In order to find the inverse of the real matrix given in problem [1, 2.7]:
we can compute the solutions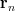 by (2, 3) for which
by (2, 3) for which 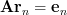 ,
,
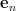 beeing the
beeing the 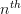 vector of the standard base ,
vector of the standard base , 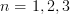 . The inverse matrix will then be
. The inverse matrix will then be ![\mathbf{R}=\left[\mathbf{r}_1 \; \mathbf{r}_2 \; \mathbf{r}_3 \right]](https://lysario.de/wp-content/cache/tex_501bf87d2cc82edd44f9db5fef79ec79.png) The Cholesky decomposition of the matrix
The Cholesky decomposition of the matrix 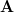 is obtained by:
is obtained by:
By equation (2) we obtain for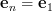 :
:
and thus by (3):
For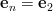 using the formula (2):
using the formula (2):
and thus by (3):
Finally for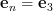 using again the formula (2):
using again the formula (2):
and thus by (3):
Thus the inverse of the matrix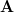 is given by
is given by
, which is exactly the solution that was obtained in [2] for problem [1, 2.7].
[1] Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”, Prentice Hall, ISBN: 0-13-598582-X.
[2] Panagiotis Chatzichrisafis: “Solution of exercise 2.7 from Kay’s Modern Spectral Estimation - Theory and Applications”, lysario.de.
Solution: The Cholesky decomposition provides a numeric approach for solving linear equations
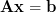 . First the matrix
. First the matrix 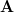 is decomposed
as a matrix product
is decomposed
as a matrix product 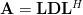 , where
, where 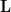 is a lower triangular matrix with the elements on the main diagonal beeing ones
is a lower triangular matrix with the elements on the main diagonal beeing ones 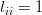 , and
, and 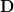 a diagonal matrix. In order to verify [1, (2.53)] we set
a diagonal matrix. In order to verify [1, (2.53)] we set 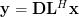 or
or
![\left[ {\begin{array}{*{20}c}
1 & 0 & \cdots & 0 \\
{l_{21} } & 1 & \cdots & 0 \\
\vdots & \vdots & \vdots & \vdots \\
{l_{n1} } & {l_{n1} } & \cdots & 1 \\
\end{array}} \right]\left[ {\begin{array}{*{20}c}
{y_1 } \\
{y_2 } \\
\vdots \\
{y_n } \\
\end{array}} \right] = \left[ {\begin{array}{*{20}c}
{b_1 } \\
{b_2 } \\
\vdots \\
{b_n } \\
\end{array}} \right]](https://lysario.de/wp-content/cache/tex_4fe2853eb9fc2bb47bc6a29b737bdb71.png) | (1) | ||
which is written analytically as:
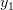 |  | 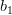 | |
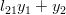 |  | 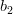 | |
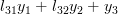 |  | 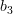 | |
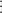 | |||
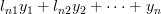 |  | 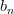 |
In order to obtain the solution for the vector
 the previous set of equations can be rewritten as
the previous set of equations can be rewritten as
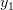 |  | 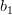 | |
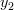 |  | 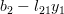 | |
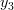 |  | 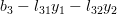 | |
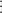 | |||
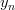 |  | 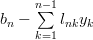 | (2) |
The last equations verify [1, (2.53)]. We had previously set
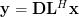 from which we can derive
the equation
from which we can derive
the equation 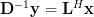 . Again expanding the previous compact matrix notation the following set of equations can be obtained:
. Again expanding the previous compact matrix notation the following set of equations can be obtained:
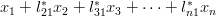 |  | 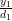 | |
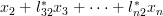 |  | 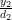 | |
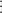 | |||
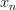 |  | 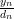 | (3) |
The solution for the vector
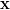 can be found by rewriting the previous set of equations:
can be found by rewriting the previous set of equations:
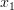 |  | 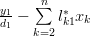 | |
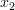 |  | 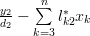 | |
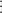 | |||
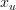 |  | 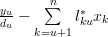 | (4) |
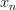 |  | 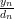 |
The set of equations (2,3) verify [1, (2.54)]. Equation [1, (2.55)] has still to be verified. This equation provides the algorithm to decompose the matrix
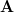 . Let
. Let ![\mathbf{L}=[l_{ij}]](https://lysario.de/wp-content/cache/tex_438a67ce1c3c41c2f40f2f5c6d46ec6e.png) with
with
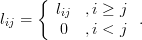 | (5) | ||
Thus
![\mathbf{L}^H=[l^H_{ij}]=[l^{*}_{ji}]= \left\{ {\begin{array}{*{20}c}
{l^{*}_{ji} } & {,j \ge i} \\
0 & {,i < j} \\
\end{array}} \right. .](https://lysario.de/wp-content/cache/tex_a12325a2a429c1a0cb9d1753bccdb1ef.png) | (6) | ||
Furthermore let
![\mathbf{D}=[d_{ij}]](https://lysario.de/wp-content/cache/tex_f8de7c8a00fbe8abeae4be76ac36c583.png) with
with
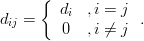 | (7) | ||
The elements of the matrix product
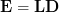 are given by
are given by
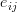 |  | 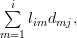 | (8) |
and the elements
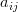 of
of 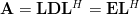 are obtained by
are obtained by 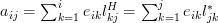 (because
(because 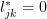 for
for 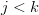 ).
When the elements
).
When the elements 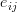 are replaced by the corresponding sum (8) then the elements
are replaced by the corresponding sum (8) then the elements 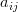 can be further expanded to:
can be further expanded to:
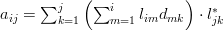 . But
. But 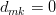 , for
, for 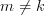 and thus:
and thus:
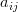 |  | 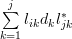 | |
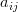 |  | 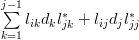 | |
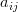 |  | 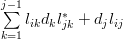 | (9) |
The last equation (9) is a consequence of the fact that
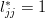 . A recursive formula for
. A recursive formula for 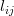 can be derived when
can be derived when 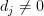 :
:
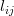 |  | 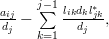 | (10) |
Equation (10) can be identified as the second part of the relation [1, (2.55)]. The first part is obtained by simply setting
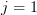 . In this case the second summand degenerates and the relation can be written as:
. In this case the second summand degenerates and the relation can be written as: 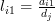 .
From (9) by setting
.
From (9) by setting 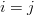 the following relation emerges:
the following relation emerges:
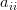 |  | 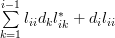 | |
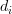 |  | 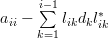 | |
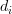 |  | 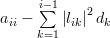 | (11) |
and again for
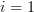 the second summand degenerates and we obtain the relation
the second summand degenerates and we obtain the relation 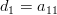 .
In order to find the inverse of the real matrix given in problem [1, 2.7]:
.
In order to find the inverse of the real matrix given in problem [1, 2.7]:
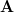 |  | ![\left[ {\begin{array}{*{20}c}
1 & { - a} & {a^2 } \\
{ - a} & 1 & { - a} \\
{a^2 } & { - a} & 1 \\
\end{array}} \right]](https://lysario.de/wp-content/cache/tex_5e04232c7a888c06e2fd06c771ae1630.png) | (12) |
we can compute the solutions
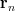 by (2, 3) for which
by (2, 3) for which 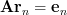 ,
,
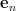 beeing the
beeing the 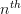 vector of the standard base ,
vector of the standard base , 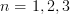 . The inverse matrix will then be
. The inverse matrix will then be ![\mathbf{R}=\left[\mathbf{r}_1 \; \mathbf{r}_2 \; \mathbf{r}_3 \right]](https://lysario.de/wp-content/cache/tex_501bf87d2cc82edd44f9db5fef79ec79.png) The Cholesky decomposition of the matrix
The Cholesky decomposition of the matrix 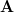 is obtained by:
is obtained by:
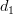 |  | 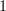 | |
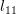 |  | 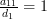 | |
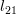 |  | 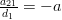 | |
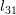 |  | 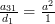 | |
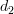 |  | 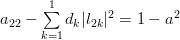 | |
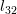 |  | 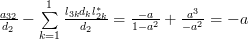 | |
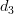 |  | 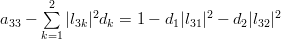 | |
 | 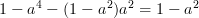 |
By equation (2) we obtain for
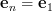 :
:
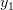 |  | 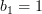 | |
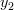 |  | 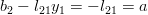 | |
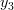 |  | 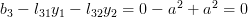 | |
and thus by (3):
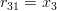 |  | 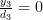 | |
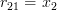 |  | 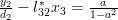 | |
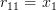 |  | 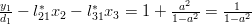 |
For
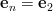 using the formula (2):
using the formula (2):
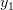 |  | 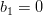 | |
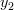 |  |  | |
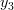 |  | 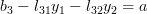 | |
and thus by (3):
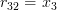 |  | 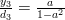 | |
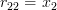 |  | 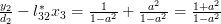 | |
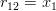 |  | 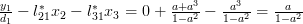 |
Finally for
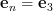 using again the formula (2):
using again the formula (2):
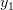 |  | 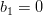 | |
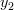 |  | 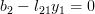 | |
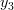 |  | 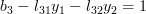 | |
and thus by (3):
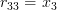 |  | 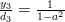 | |
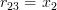 |  | 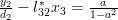 | |
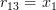 |  | 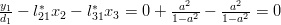 |
Thus the inverse of the matrix
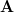 is given by
is given by
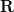 |  | ![\left[ {\begin{array}{*{20}c}
\frac{1}{1-a^2} & {\frac{a}{1-a^2}} & {0 } \\
{\frac{a}{1-a^2}} & \frac{1+a^2}{1-a^2} & {\frac{a}{1-a^2}} \\
{0 } & {\frac{a}{1-a^2}} & \frac{1}{1-a^2} \\
\end{array}} \right]](https://lysario.de/wp-content/cache/tex_9ba0fb20a31488145591508dfedfc986.png) | (13) |
 | ![\frac{1}{(1-a^2)^2}\left[ {\begin{array}{*{20}c}
1-a^2 & a-a^3 & 0 \\
a-a^3 & 1-a^4 & a-a^3 \\
0 & a-a^3 & 1-a^2 \\
\end{array}} \right]](https://lysario.de/wp-content/cache/tex_5445fcda9b3586ed6b29283a37e53eb7.png) | (14) |
, which is exactly the solution that was obtained in [2] for problem [1, 2.7].
[1] Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”, Prentice Hall, ISBN: 0-13-598582-X.
[2] Panagiotis Chatzichrisafis: “Solution of exercise 2.7 from Kay’s Modern Spectral Estimation - Theory and Applications”, lysario.de.
One Response for "Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”,p. 34 exercise 2.12"
[...] matrix , assuming are the elements of the matrix , are given by [1, p.30, (2.55)] (see also [3, relations (10) and (11) ]): and the elements of the matrix are given by the relation: The corresponding [...]
Leave a reply