Lysario – by Panagiotis Chatzichrisafis
"ούτω γάρ ειδέναι το σύνθετον υπολαμβάνομεν, όταν ειδώμεν εκ τίνων και πόσων εστίν …"
Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”,p. 62 exercise 3.14
Author: Panagiotis4 Mrz
In [1, p. 62 exercise 3.14] it is requested to proof prove that the autocorrelation matrix given by [1, eq. 3.46] is also positive semidefinite. This shall be done by usage of the definition of the semidefinite property of the ACF in [1, eq. 3.45].
Solution: A matrix is positive semidefinite if
is positive semidefinite if 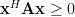 . And the autocorrelation matrix given by ([1, eq. 3.46]) is:
. And the autocorrelation matrix given by ([1, eq. 3.46]) is:
Let![\mathbf{\alpha}=\left[\begin{array}{ccc} \alpha[0]&\cdots & \alpha[M-1]\end{array}\right]^{T}](https://lysario.de/wp-content/cache/tex_db77574db1c39db608938a23ba39f3ac.png) and
and ![\mathbf{x}=\left[\begin{array}{ccc} x[0]&\cdots & x[M-1]\end{array}\right]^{T}](https://lysario.de/wp-content/cache/tex_3ad1323a652486170276ebae7309e359.png) then from [1, eq. 3.45] we obtain:
then from [1, eq. 3.45] we obtain:
Thus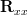 is positive semidefinite. QED.
is positive semidefinite. QED.
[1] Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”, Prentice Hall, ISBN: 0-13-598582-X.
Solution: A matrix
 is positive semidefinite if
is positive semidefinite if 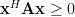 . And the autocorrelation matrix given by ([1, eq. 3.46]) is:
. And the autocorrelation matrix given by ([1, eq. 3.46]) is:
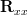 |  | 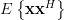 | (1) |
 | ![\left[\begin{array}{cccc}r_{xx}[0] & r_{xx}[-1]& \cdots&r_{xx}[-(M-1)] \\r_{xx}[1] &r_{xx}[0] &\cdots&r_{xx}[-(M-2)] \\ \vdots &\vdots & \ddots& \vdots \\ r_{xx}[M-1]&r_{xx}[M-2]&... &r_{xx}[0]\end{array}\right]](https://lysario.de/wp-content/cache/tex_e9b7e66c0985bdded8600db8a43eb912.png) | (2) |
Let
![\mathbf{\alpha}=\left[\begin{array}{ccc} \alpha[0]&\cdots & \alpha[M-1]\end{array}\right]^{T}](https://lysario.de/wp-content/cache/tex_db77574db1c39db608938a23ba39f3ac.png) and
and ![\mathbf{x}=\left[\begin{array}{ccc} x[0]&\cdots & x[M-1]\end{array}\right]^{T}](https://lysario.de/wp-content/cache/tex_3ad1323a652486170276ebae7309e359.png) then from [1, eq. 3.45] we obtain:
then from [1, eq. 3.45] we obtain:
![E\left\{\left| \sum\limits_{n=0}^{M-1}\alpha^{\ast}[n]x[n] \right|^{2}\right\}](https://lysario.de/wp-content/cache/tex_94939c885e05cffbd2a2b30654c3ae15.png) | 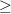 | 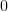 | |
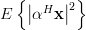 | 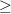 | 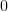 | |
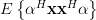 | 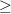 | 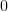 | |
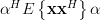 | 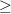 | 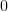 | |
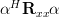 | 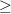 | 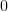 |
Thus
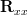 is positive semidefinite. QED.
is positive semidefinite. QED. [1] Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”, Prentice Hall, ISBN: 0-13-598582-X.
Leave a reply