Lysario – by Panagiotis Chatzichrisafis
"ούτω γάρ ειδέναι το σύνθετον υπολαμβάνομεν, όταν ειδώμεν εκ τίνων και πόσων εστίν …"
Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”,p. 61 exercise 3.5
Author: Panagiotis11 Jan
In [1, p. 61 exercise 3.5] we are asked to show that for the conditions of Problem [1, p. 60, exercise 3.4] the CR bound is
and further to give a statement about the efficiency of the sample mean estimator.
Solution: The Cramer Rao bound of the variance of an estimated parameter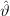 of a propability density function
of a propability density function 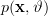 which is obtained from samples of the random variables
which is obtained from samples of the random variables  is obtained by the formula [1, p. 46, (3.17),(3.18)] :
is obtained by the formula [1, p. 46, (3.17),(3.18)] :
Because the samples {x[0],…,x[n-1]} are independent random variables with normal distribution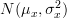 the joint propability density function is given by:
the joint propability density function is given by:
thus:
From the previous relation and (1) we obtain the result that the Cramer Rao bound of the variance of the mean estimation is bounded by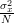 :
:
We had computed in [2, relation (5)] that the variance of the estimator of the mean![\hat{\mu}_x=\frac{1}{N}\sum_{i=0}^{N-1}x[i]](https://lysario.de/wp-content/cache/tex_5f6517cac0e6bbcf753702a383c312cf.png) is given by
is given by 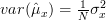 . Thus the sample mean
. Thus the sample mean ![\hat{\mu}_x=\frac{1}{N}\sum_{i=0}^{N-1}x[i]](https://lysario.de/wp-content/cache/tex_5f6517cac0e6bbcf753702a383c312cf.png) is an efficient estimator of the mean.
is an efficient estimator of the mean.
[1] Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”, Prentice Hall, ISBN: 0-13-598582-X.
[2] Chatzichrisafis: “Solution of exercise 3.4 from Kay’s Modern Spectral Estimation - Theory and Applications”.
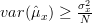 | |||
and further to give a statement about the efficiency of the sample mean estimator.
Solution: The Cramer Rao bound of the variance of an estimated parameter
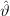 of a propability density function
of a propability density function 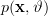 which is obtained from samples of the random variables
which is obtained from samples of the random variables  is obtained by the formula [1, p. 46, (3.17),(3.18)] :
is obtained by the formula [1, p. 46, (3.17),(3.18)] :
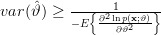 | (1) | ||
Because the samples {x[0],…,x[n-1]} are independent random variables with normal distribution
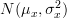 the joint propability density function is given by:
the joint propability density function is given by:
![f(\mathbf{x}) =\prod_{i=0}^{N-1}\left(\frac{1}{\sqrt{2\pi}\sigma_x}e^{-\frac{1}{2}\left(\frac{x[i]-\mu_x}{\sigma_x}\right)}\right)](https://lysario.de/wp-content/cache/tex_f5d4ff1b095198b3df935d18cb631a7f.png) | (2) | ||
thus:
 |  | ![-\ln(\sqrt{2\pi}\sigma_x) N-\frac{1}{2}\sum\limits_{i=0}^{N-1}\left(\frac{x[i]-\mu_x}{\sigma_x}\right)^2 \Rightarrow](https://lysario.de/wp-content/cache/tex_1aeb8e6050347cb31a6aeda696e0e7da.png) | (3) |
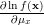 |  | ![\sum\limits_{i=0}^{N-1}\left(\frac{x[i]-\mu_x}{\sigma_x^2}\right) \Rightarrow](https://lysario.de/wp-content/cache/tex_3f3b4047806e4fe03e965387b9751e40.png) | |
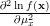 |  | 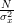 |
From the previous relation and (1) we obtain the result that the Cramer Rao bound of the variance of the mean estimation is bounded by
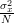 :
:
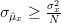 | (4) | ||
We had computed in [2, relation (5)] that the variance of the estimator of the mean
![\hat{\mu}_x=\frac{1}{N}\sum_{i=0}^{N-1}x[i]](https://lysario.de/wp-content/cache/tex_5f6517cac0e6bbcf753702a383c312cf.png) is given by
is given by 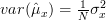 . Thus the sample mean
. Thus the sample mean ![\hat{\mu}_x=\frac{1}{N}\sum_{i=0}^{N-1}x[i]](https://lysario.de/wp-content/cache/tex_5f6517cac0e6bbcf753702a383c312cf.png) is an efficient estimator of the mean.
is an efficient estimator of the mean.
[1] Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”, Prentice Hall, ISBN: 0-13-598582-X.
[2] Chatzichrisafis: “Solution of exercise 3.4 from Kay’s Modern Spectral Estimation - Theory and Applications”.
2 Responses for "Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”,p. 61 exercise 3.5"
[...] with normal distribution and the natural logarithm of the joint pdf is given by from cite[ relation (3) ]{Chatzichrisafis352010}: From this relation we can find the gradient in respect to the vector [...]
[...] 25 Apr In [1, p. 61 exercise 3.7] we are asked to find the MLE of and . for the conditions of Problem [1, p. 60 exercise 3.4] (see also [2, solution of exercise 3.4]). We are asked if the MLE of the parameters are asymptotically unbiased , efficient and Gaussianly distributed. Solution: The p.d.f of the observations is given by With and . Thus the determinant is given by . Furthermore we can simplify For a given measurement we obtain the likelihood function: (1) Obviously the previous equation is positive and thus the estimator of the mean which will maximize the probability of the observation will provide a local maximum at the points where the derivative in respect to will be zero. Because the function is positive we can also use the natural logarithm of the likelihood function (the log-likelihood function) in order to obtain the maximum likelihood of . This was already derived in [3, relation (3)]: [...]
Leave a reply