Lysario – by Panagiotis Chatzichrisafis
"ούτω γάρ ειδέναι το σύνθετον υπολαμβάνομεν, όταν ειδώμεν εκ τίνων και πόσων εστίν …"
Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”,p. 60 exercise 3.4
Author: Panagiotis28 Dez
In [1, p. 60 exercise 3.4] we are asked to prove that the estimate
is an unbiased estimator, given![\left\{x[0],x[1],...,x[N]\right\}](https://lysario.de/wp-content/cache/tex_1cc48dbb4a4db05229880d4eafd1756b.png) are independent and identically distributed according to a
are independent and identically distributed according to a 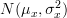 distribution. Furthermore we are asked to also find the variance of the estimator.
distribution. Furthermore we are asked to also find the variance of the estimator.
Solution: The mean of the estimator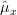 is given by
is given by
Thus the estimator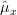 is unbiased. The variance of the estimator about the mean
is unbiased. The variance of the estimator about the mean 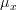 is given by:
is given by:
Considering the fact that the samples are independent we can set![E\{x[n]x[k]\}=E\{x[n]\}E\{x[k]\}=\mu^2_x](https://lysario.de/wp-content/cache/tex_051237e59c44de24ff7741d385b52df1.png) for
for 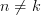 and obtain
and obtain
Thus it remains to obain the value of![E\{x^2[n]\}](https://lysario.de/wp-content/cache/tex_146af3daf0adb7dfe89991c6250647f2.png) in order to determine the variance of the estimator. We can determine
in order to determine the variance of the estimator. We can determine ![E\{x^2[n]\}](https://lysario.de/wp-content/cache/tex_146af3daf0adb7dfe89991c6250647f2.png) by the variance
by the variance 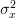 of
of ![x[n]](https://lysario.de/wp-content/cache/tex_d3baaa3204e2a03ef9528a7d631a4806.png) :
:
And thus the variance of the estimator (2), considering (3) and (4), is given by:
We have proved thus that the estimator is unbiased and have obtained the variance of the estimator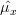 . QED.
. QED.
[1] Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”, Prentice Hall, ISBN: 0-13-598582-X.
![\hat{\mu}_x = \frac{1}{N}\sum\limits^{N-1}_{n=0}x[n]](https://lysario.de/wp-content/cache/tex_fdf7f47786a09a823706c0185f0d813a.png) | (1) | ||
is an unbiased estimator, given
![\left\{x[0],x[1],...,x[N]\right\}](https://lysario.de/wp-content/cache/tex_1cc48dbb4a4db05229880d4eafd1756b.png) are independent and identically distributed according to a
are independent and identically distributed according to a 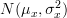 distribution. Furthermore we are asked to also find the variance of the estimator.
distribution. Furthermore we are asked to also find the variance of the estimator.
Solution: The mean of the estimator
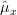 is given by
is given by
 |  | ![\frac{1}{N}\sum\limits^{N-1}_{n=0}E\left\{x[n]\right\}](https://lysario.de/wp-content/cache/tex_3395b02598d7baf0eb8e3ca6852aed8d.png) | |
 |  | ||
 | 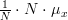 | ||
 | 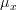 |
Thus the estimator
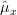 is unbiased. The variance of the estimator about the mean
is unbiased. The variance of the estimator about the mean 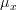 is given by:
is given by:
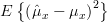 |  | 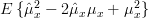 | |
 | 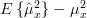 | ||
 | ![E\left\{(\frac{1}{N}\sum\limits^{N-1}_{n=0}x[n])(\frac{1}{N}\sum\limits^{N-1}_{k=0}x[k])\right\}-\mu^2_x](https://lysario.de/wp-content/cache/tex_e48f7764c4c4a7d2508dbe950de05ebf.png) | ||
 | ![\frac{1}{N^2}\sum\limits^{N-1}_{n=0}\sum\limits^{N-1}_{k=0}E\{x[n]x[k]\} -\mu^2_x](https://lysario.de/wp-content/cache/tex_27f9deeb3c452ac515e4e8f49f9fa3e1.png) | (2) |
Considering the fact that the samples are independent we can set
![E\{x[n]x[k]\}=E\{x[n]\}E\{x[k]\}=\mu^2_x](https://lysario.de/wp-content/cache/tex_051237e59c44de24ff7741d385b52df1.png) for
for 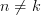 and obtain
and obtain
![\sum\limits^{N-1}_{n=0}\sum\limits^{N-1}_{k=0}E\{x[n]x[k]\}](https://lysario.de/wp-content/cache/tex_6d9555eaba2817fc85573b9329207e77.png) |  | ![\sum\limits^{N-1}_{n=0}E\{x^2[n]\}](https://lysario.de/wp-content/cache/tex_b313647d2320a1f1d5b137bf3875688f.png) | |
 | ![+{\sum\limits^{N-1}_{n=0, n \neq k}\sum\limits^{N-1}_{k=0}}E\{x[n]\}E\{x[k]\}](https://lysario.de/wp-content/cache/tex_d458dc8618ab96ab43455b43dea410c9.png) | ||
 | ![N \cdot E\{x^2[n]\} +N(N-1)\mu^2_x](https://lysario.de/wp-content/cache/tex_d9ccfa24f8cf96207d09785c3ef91dc9.png) | (3) |
Thus it remains to obain the value of
![E\{x^2[n]\}](https://lysario.de/wp-content/cache/tex_146af3daf0adb7dfe89991c6250647f2.png) in order to determine the variance of the estimator. We can determine
in order to determine the variance of the estimator. We can determine ![E\{x^2[n]\}](https://lysario.de/wp-content/cache/tex_146af3daf0adb7dfe89991c6250647f2.png) by the variance
by the variance 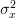 of
of ![x[n]](https://lysario.de/wp-content/cache/tex_d3baaa3204e2a03ef9528a7d631a4806.png) :
:
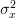 |  | ![E\{(x[n]-\mu_x)^2\}](https://lysario.de/wp-content/cache/tex_a02a935b8c2c5558871b29888ec4c9ba.png) | |
 | ![E\{x^2[n]\}-\mu^2_x \Rightarrow](https://lysario.de/wp-content/cache/tex_89b620843608ba6138661ebd084b6efc.png) | ||
![E\{x^2[n]\}](https://lysario.de/wp-content/cache/tex_146af3daf0adb7dfe89991c6250647f2.png) |  | 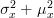 | (4) |
And thus the variance of the estimator (2), considering (3) and (4), is given by:
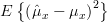 |  | 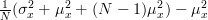 | |
 | 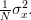 | (5) |
We have proved thus that the estimator is unbiased and have obtained the variance of the estimator
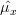 . QED.
. QED.[1] Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”, Prentice Hall, ISBN: 0-13-598582-X.
2 Responses for "Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”,p. 60 exercise 3.4"
[...] Rao bound of the variance of the mean estimation is bounded by : (3) We had computed in [2, (5)] that the variance of the estimator of the mean is given by . Thus the sample mean is an [...]
[...] Spectral Estimation – Theory and Applications”, Prentice Hall, ISBN: 0-13-598582-X. [2] Chatzichrisafis: “Solution of exercise 3.4 from Kay’s Modern Spectral Estimation – Theor… [3] Granino A. Korn and Theresa M. Korn: “Mathematical Handbook for Scientists and [...]
Leave a reply