Lysario – by Panagiotis Chatzichrisafis
"ούτω γάρ ειδέναι το σύνθετον υπολαμβάνομεν, όταν ειδώμεν εκ τίνων και πόσων εστίν …"
Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”,p. 34 exercise 2.13
Author: Panagiotis27 Apr
In [1, p. 34 exercise 2.13] we are asked to consider the problem of fitting the data ![\left\{x[0],...,x[N-1]\right\}](https://lysario.de/wp-content/cache/tex_9ceb2dd63d7268e57f2b85d862426d56.png) by the sum of a dc signal and a sinusoid as:
by the sum of a dc signal and a sinusoid as:
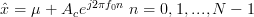 . The complex dc level
. The complex dc level 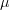 and the sinusoidal amplitude
and the sinusoidal amplitude 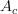 are unknown and we are notified that we may view the determination of
are unknown and we are notified that we may view the determination of 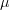 ,
, 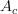 as the solution of the overdetermined set of equations.
as the solution of the overdetermined set of equations.
It is asked to find the least squares solution for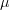 and
and 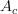 . If furthermore
. If furthermore 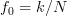 , where
, where 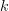 is a nonzero integer in the range
is a nonzero integer in the range ![[-N/2,N/2-1]](https://lysario.de/wp-content/cache/tex_3a5bf53d3e9902f7fffe9d68b2de1428.png) for
for 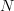 even and
even and ![[-(N-1)/2,(N-1)/2]](https://lysario.de/wp-content/cache/tex_dde8f99f860237fa0b573d2ad067620a.png) for
for 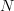 odd we are asked to determine again the least squares solution.
odd we are asked to determine again the least squares solution.
Solution: The least square solution of a overdetermined system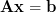 is given by [1, p.30, (2.57)]:
is given by [1, p.30, (2.57)]:
The summations are equal to
and
as they are both geometric sums [2, p.16] of the form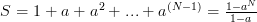 with
with 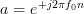 in the one case and
in the one case and 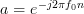 in the second case.
The estimation of the mean and the amplitude is thus given by:
in the second case.
The estimation of the mean and the amplitude is thus given by:
If furthermore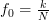 ,
, 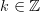 as described in the problem statement then both sums (3), (6) are equal to zero because
as described in the problem statement then both sums (3), (6) are equal to zero because 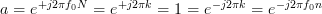 .
In this case the least squares solution of the overdetermined system is given by:
.
In this case the least squares solution of the overdetermined system is given by:
[1] Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”, Prentice Hall, ISBN: 0-13-598582-X.
[2] Bronstein and Semdjajew and Musiol and Muehlig: “Taschenbuch der Mathematik”, Verlag Harri Deutsch Thun und Frankfurt am Main, ISBN: 3-8171-2003-6.
![\left\{x[0],...,x[N-1]\right\}](https://lysario.de/wp-content/cache/tex_9ceb2dd63d7268e57f2b85d862426d56.png) by the sum of a dc signal and a sinusoid as:
by the sum of a dc signal and a sinusoid as:
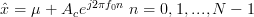 . The complex dc level
. The complex dc level 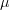 and the sinusoidal amplitude
and the sinusoidal amplitude 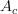 are unknown and we are notified that we may view the determination of
are unknown and we are notified that we may view the determination of 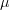 ,
, 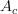 as the solution of the overdetermined set of equations.
as the solution of the overdetermined set of equations.
![\left[\begin{array}{cc}1 & 1 \\ 1 & e^{j2\pi f_{0}} \\ \vdots & \vdots \\ 1 & e^{j2\pi f_{0}(N-1)}\end{array} \right] \cdot \left[\begin{array}{c}\mu \\ A_{c} \end{array} \right] = \left[\begin{array}{c}x[0] \\ \vdots \\ x[N-1] \end{array} \right].](https://lysario.de/wp-content/cache/tex_bf7d1a9edfb68f8a07beb5ca2929cbc6.png) | (1) | ||
It is asked to find the least squares solution for
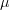 and
and 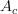 . If furthermore
. If furthermore 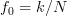 , where
, where 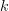 is a nonzero integer in the range
is a nonzero integer in the range ![[-N/2,N/2-1]](https://lysario.de/wp-content/cache/tex_3a5bf53d3e9902f7fffe9d68b2de1428.png) for
for 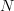 even and
even and ![[-(N-1)/2,(N-1)/2]](https://lysario.de/wp-content/cache/tex_dde8f99f860237fa0b573d2ad067620a.png) for
for 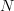 odd we are asked to determine again the least squares solution.
odd we are asked to determine again the least squares solution.
Solution: The least square solution of a overdetermined system
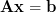 is given by [1, p.30, (2.57)]:
is given by [1, p.30, (2.57)]:
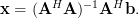 | (2) | ||
![\left[\begin{array}{c}\mu \\ A_{c} \end{array} \right]](https://lysario.de/wp-content/cache/tex_762cab2071f672d308a64b0b4060494d.png) |  | ![\left( \left[\begin{array}{ccc} 1 & \cdots & 1 \\ 1 & \cdots & e^{-j2\pi f_{0}(N-1)}\end{array} \right] \cdot \left[\begin{array}{cc} 1 & 1 \\ 1 & e^{j2\pi f_{0}} \\ \vdots & \vdots \\ 1 & e^{j2\pi f_{0}(N-1)}\end{array} \right] \right)^{-1} \cdot](https://lysario.de/wp-content/cache/tex_8c6a357dcf9b0d45e582f5e5884736c1.png) | |
 | ![\cdot \left[ \begin{array}{cccc}
1 & 1 & \cdots & 1 \\ 1 & e^{-j2\pi f_{0}} & \cdots & e^{-j2\pi f_{0}(N-1)}
\end{array}\right]
\left[ \begin{array}{c}
x[0] \\
\vdots \\
x[N-1]
\end{array} \right]](https://lysario.de/wp-content/cache/tex_9d29cf4c400f0a7757ee6a3f3c6b7fae.png) | ||
 | ![\left[\begin{array}{cc} N & \sum\limits_{n=0}^{N-1} e^{+j2\pi f_{0} n} \\ \sum\limits_{n=0}^{N-1} e^{-j2\pi f_{0} n} & N \end{array}\right]^{-1} \cdot \left[\begin{array}{c}\sum\limits_{n=0}^{N-1} x[n] \\ \sum\limits_{n=0}^{N-1} x[n] e^{-j2\pi f_{0} n}\end{array}\right]](https://lysario.de/wp-content/cache/tex_7c85e078b332acf6badf72088de8ccac.png) |
The summations are equal to
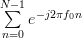 |  | 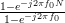 | (3) |
 | 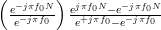 | (4) | |
 | 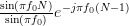 | (5) |
and
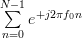 |  | 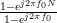 | (6) |
 | 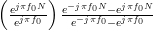 | (7) | |
 | 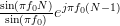 | (8) |
as they are both geometric sums [2, p.16] of the form
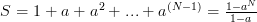 with
with 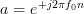 in the one case and
in the one case and 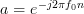 in the second case.
The estimation of the mean and the amplitude is thus given by:
in the second case.
The estimation of the mean and the amplitude is thus given by:
![\left[\begin{array}{c}\mu \\ A_{c} \end{array} \right]](https://lysario.de/wp-content/cache/tex_762cab2071f672d308a64b0b4060494d.png) |  | 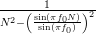 | |
 | ![\cdot \left[\begin{array}{cc} N &- \frac{\sin(\pi f_{0} N)e^{j\pi f_{0} (N-1)}}{\sin(\pi f_{0}) } \\ -\frac{\sin(\pi f_{0} N)e^{-j\pi f_{0} (N-1)}}{\sin(\pi f_{0})} & N \end{array}\right]](https://lysario.de/wp-content/cache/tex_79357e491805c6c5909150e836cce8bb.png) | ||
 | ![\cdot \left[\begin{array}{c} \sum\limits_{n=0}^{N-1} x[n] \\ \sum\limits_{n=0}^{N-1} x[n] e^{-j2\pi f_{0} n} \end{array} \right]](https://lysario.de/wp-content/cache/tex_c5ba8ad323298f8b135d8609fd291077.png) | (9) |
If furthermore
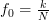 ,
, 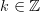 as described in the problem statement then both sums (3), (6) are equal to zero because
as described in the problem statement then both sums (3), (6) are equal to zero because 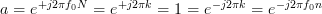 .
In this case the least squares solution of the overdetermined system is given by:
.
In this case the least squares solution of the overdetermined system is given by:
![\left[\begin{array}{c}\mu \\ A_{c} \end{array} \right]](https://lysario.de/wp-content/cache/tex_762cab2071f672d308a64b0b4060494d.png) |  | ![\left[\begin{array}{c}\frac{1}{N} \sum\limits_{n=0}^{N-1} x[n] \\ \frac{1}{N}\sum\limits_{n=0}^{N-1} x[n] e^{-j2\pi f_{0} n} \end{array}\right] = \left[\begin{array}{c}\frac{1}{N} \sum\limits_{n=0}^{N-1} x[n] \\ X(k) \end{array}\right].](https://lysario.de/wp-content/cache/tex_cd648bb380ca6dc369bad890e72474ca.png) |
[1] Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”, Prentice Hall, ISBN: 0-13-598582-X.
[2] Bronstein and Semdjajew and Musiol and Muehlig: “Taschenbuch der Mathematik”, Verlag Harri Deutsch Thun und Frankfurt am Main, ISBN: 3-8171-2003-6.
Leave a reply