Lysario – by Panagiotis Chatzichrisafis
"ούτω γάρ ειδέναι το σύνθετον υπολαμβάνομεν, όταν ειδώμεν εκ τίνων και πόσων εστίν …"
Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”,p. 34 exercise 2.5
Author: Panagiotis13 Jun
In exercise [1, p. 34 exercise 2.5] we are asked to show that
the matrix 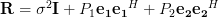 is circulant
when
is circulant
when ![\mathbf{e_i}^H=\left[ {\begin{array}{*{20}c}
1 & {e^{-j2\pi f_i } } & {e^{-j2\pi (2f_i) } } & \cdots & {e^{-j2\pi (n - 1)f_i } }
\end{array}} \right], i=1,2](https://lysario.de/wp-content/cache/tex_38ce66bc9234a41f314618cd54d2cfd9.png) .
.
Solution: A matrix is circulant when its elements are arranged in the following way:
is circulant when its elements are arranged in the following way:
Computing the dyad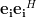 (for
(for 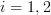 ) results in
) results in
We observe that this is a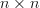 hermitian toeplitz matrix.
In order to be circulant the elements
hermitian toeplitz matrix.
In order to be circulant the elements 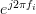 and
and 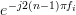 ,
, 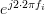 and
and 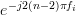 , etc. have to be equal. Or in general that the following relation must hold:
, etc. have to be equal. Or in general that the following relation must hold:
Because [1, p.22]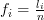 ,
, 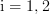 where
where 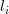 are distinct integers in the range
are distinct integers in the range ![[-n/2,n/2-1]](https://lysario.de/wp-content/cache/tex_24916734a0a5230271c84429761581eb.png) for
for  even or [-(n-1)/2, (n-1)/2] for
even or [-(n-1)/2, (n-1)/2] for  odd we can rewrite the right hand side of (2) as:
odd we can rewrite the right hand side of (2) as:
But
thus
which proofs that the dyad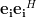 is circulant because relation (2) is satisfied. The matrix
is circulant because relation (2) is satisfied. The matrix 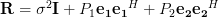 is circulant, as the product of a circulant matrix with a scalar is itself a circulant matrix, the identity matrix is a special form of a circulant matrix, and also the sum of circulant matrices is also a circulant matrix. QED.
is circulant, as the product of a circulant matrix with a scalar is itself a circulant matrix, the identity matrix is a special form of a circulant matrix, and also the sum of circulant matrices is also a circulant matrix. QED.
[1] Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”, Prentice Hall, ISBN: 0-13-598582-X.
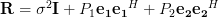 is circulant
when
is circulant
when ![\mathbf{e_i}^H=\left[ {\begin{array}{*{20}c}
1 & {e^{-j2\pi f_i } } & {e^{-j2\pi (2f_i) } } & \cdots & {e^{-j2\pi (n - 1)f_i } }
\end{array}} \right], i=1,2](https://lysario.de/wp-content/cache/tex_38ce66bc9234a41f314618cd54d2cfd9.png) .
.
Solution: A matrix
 is circulant when its elements are arranged in the following way:
is circulant when its elements are arranged in the following way:
![A=\left[ {\begin{array}{*{20}c}
{a_0 } & {a_1 } & \cdots & {a_{n - 1} } \\
{a_{n - 1} } & {a_0 } & \cdots & {a_{n - 2} } \\
\vdots & \vdots & \vdots & \vdots \\
{a_1 } & {a_2 } & \cdots & {a_0 } \\
\end{array}} \right]](https://lysario.de/wp-content/cache/tex_2b422c5c30c9533b4bf67b5501456a01.png) | (1) | ||
Computing the dyad
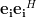 (for
(for 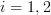 ) results in
) results in
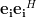 |  | ![\left[ {\begin{array}{*{20}c}
1 \\
{e^{j2\pi f_i } } \\
\vdots \\
{e^{j2\pi (n - 1)f_i } } \\
\end{array}} \right] \cdot \left[ {\begin{array}{*{20}c}
1 & {e^{-j2\pi f_i } } & \cdots & {e^{-j2\pi (n - 1)f_i } }
\end{array}} \right]](https://lysario.de/wp-content/cache/tex_a35cf44b822894485b99a828cddb6e71.png) | |
 | ![\left[ {\begin{array}{*{20}c}
1 & {e^{ - j2\pi f_i } } & {e^{ - j2 \cdot 2\pi f_i } } & \cdots & {e^{ - j2(n - 1)\pi f_i } } \\
{e^{j2\pi f_i } } & 1 & \cdots & \cdots & {e^{ - j2(n - 2)\pi f_i } } \\
{e^{j2 \cdot 2\pi f_i } } & {e^{j2\pi f_i } } & 1 & \cdots & {e^{ - j2(n - 3)\pi f_i } } \\
\vdots & \vdots & \vdots & \vdots & \vdots \\
{e^{j2(n - 1)\pi f_i } } & {e^{j2(n - 2)\pi f_i } } & {e^{j2(n - 3)\pi f_i } } & \cdots & 1 \\
\end{array}} \right]](https://lysario.de/wp-content/cache/tex_18b20bfa5a392369243c4ccc08e03915.png) |
We observe that this is a
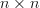 hermitian toeplitz matrix.
In order to be circulant the elements
hermitian toeplitz matrix.
In order to be circulant the elements 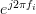 and
and 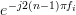 ,
, 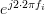 and
and 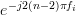 , etc. have to be equal. Or in general that the following relation must hold:
, etc. have to be equal. Or in general that the following relation must hold:
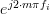 |  | 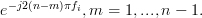 | (2) |
Because [1, p.22]
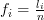 ,
, 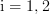 where
where 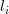 are distinct integers in the range
are distinct integers in the range ![[-n/2,n/2-1]](https://lysario.de/wp-content/cache/tex_24916734a0a5230271c84429761581eb.png) for
for  even or [-(n-1)/2, (n-1)/2] for
even or [-(n-1)/2, (n-1)/2] for  odd we can rewrite the right hand side of (2) as:
odd we can rewrite the right hand side of (2) as:
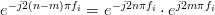 | (3) | ||
But
 | (4) | ||
thus
 | (5) | ||
which proofs that the dyad
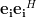 is circulant because relation (2) is satisfied. The matrix
is circulant because relation (2) is satisfied. The matrix 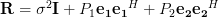 is circulant, as the product of a circulant matrix with a scalar is itself a circulant matrix, the identity matrix is a special form of a circulant matrix, and also the sum of circulant matrices is also a circulant matrix. QED.
is circulant, as the product of a circulant matrix with a scalar is itself a circulant matrix, the identity matrix is a special form of a circulant matrix, and also the sum of circulant matrices is also a circulant matrix. QED. [1] Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”, Prentice Hall, ISBN: 0-13-598582-X.
Leave a reply