Lysario – by Panagiotis Chatzichrisafis
"ούτω γάρ ειδέναι το σύνθετον υπολαμβάνομεν, όταν ειδώμεν εκ τίνων και πόσων εστίν …"
Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”,p. 34 exercise 2.4
Author: Panagiotis1 Feb
The exercise [1, p. 34 exercise 2.4] asks to show that if  is a full rank
is a full rank 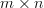 matrix with
matrix with 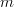 >
>  ,
,  is a
is a 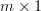 vector, and
vector, and  is an
is an 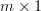 vector, that the effect of the linear transformation
vector, that the effect of the linear transformation
is to project onto the subspace spanned by the columns of
onto the subspace spanned by the columns of  . Specifically, if
. Specifically, if 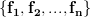 are the columns of
are the columns of  , the exercise [1, p. 34 exercise 2.4] asks to show that
, the exercise [1, p. 34 exercise 2.4] asks to show that
Furthermore it is asked why the transform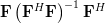 must be idempotent.
Solution: Let
must be idempotent.
Solution: Let 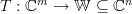 be the linear transform to which the matrix
be the linear transform to which the matrix 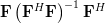 is associated to. We are asked to show that the linear transform is surjective (onto) to
is associated to. We are asked to show that the linear transform is surjective (onto) to 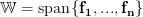 .
This linear transform can be thought as the composite of the linear transforms [2, p. 49, proposition 6.3]
.
This linear transform can be thought as the composite of the linear transforms [2, p. 49, proposition 6.3]
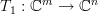 ,
,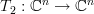 ,
,
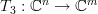 to which the matrices
to which the matrices 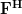 ,
,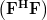 and
and  are associated respectively. We note that
are associated respectively. We note that 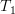 is surjective as the rank of the matrix equals
is surjective as the rank of the matrix equals  :
: 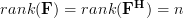 . Thus the whole image
. Thus the whole image 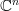 is spanned by this transform per definition. The transform
is spanned by this transform per definition. The transform 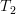 is bijective as an invertible matrix is associated with it. Therefore
is bijective as an invertible matrix is associated with it. Therefore 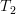 is also surjective to
is also surjective to 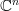 . From this we conclude that the standard basis
. From this we conclude that the standard basis 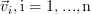 (
(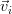 is the vector composed of zeros at all elements except the
is the vector composed of zeros at all elements except the 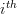 that is equal to one)
is also included in the image of
that is equal to one)
is also included in the image of 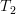 .
Because any vector
.
Because any vector 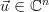 can be represented as a weighted sum of the standard basis:
can be represented as a weighted sum of the standard basis: 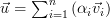 we obtain applying the linear transform
we obtain applying the linear transform 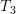 to this vector the following relation:
to this vector the following relation:
Now let be the matrix of the transform
be the matrix of the transform 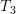 relative to the standard bases
relative to the standard bases 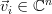 with
with 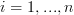 and
and 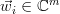 ,
, 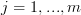 .
If the elements of the matrix are
.
If the elements of the matrix are 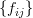 then the transform
then the transform 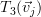 can be rewritten as [2, p. 47]:
can be rewritten as [2, p. 47]: 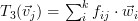 . This is simply the vector composed of the elements of the
. This is simply the vector composed of the elements of the 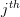 column of the matrix
column of the matrix  . This vector will be denoted as
. This vector will be denoted as 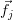 . Using matrix notation
. Using matrix notation 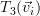 can be written simply as
can be written simply as 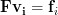 .
Thus
.
Thus 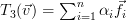 , which means that the image of
, which means that the image of 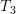 is composed of all linear combination of the columns of the corresponding matrix, this is per definition
is composed of all linear combination of the columns of the corresponding matrix, this is per definition 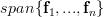 and thus the composite of the transforms
and thus the composite of the transforms 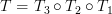 is surjective (onto) to
is surjective (onto) to 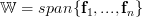 .
Now let us proceed to show that
.
Now let us proceed to show that
First we will compute the hermitian transpose of the column vector . By using the associative property of matrix multiplication and the rule [1, p. 23]
. By using the associative property of matrix multiplication and the rule [1, p. 23] 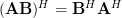 we derive the following relations:
we derive the following relations:
Now instead of multiplying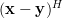 by one column
by one column 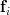 of the matrix
of the matrix ![\mathbf{F}=[\mathbf{f}_1 \cdots \mathbf{f}_i \cdots \mathbf{f}_n]](https://lysario.de/wp-content/cache/tex_6d210d4ed04bcea478b5e5437ecb3cdc.png) , as in (3),
we will proceed compute the multiplication with the whole matrix, effectiveley using all columns
, as in (3),
we will proceed compute the multiplication with the whole matrix, effectiveley using all columns 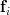 . Furthermore applying also (4) we obtain:
. Furthermore applying also (4) we obtain:
A matrix is idempotent by definition [1, p.21] when
is idempotent by definition [1, p.21] when 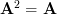 . Multiplying
. Multiplying 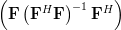 by itself and using again the associative property of matrix multiplication results in:
by itself and using again the associative property of matrix multiplication results in:
which proves that the matrix is idempotent. While this finding may be used to answer the question why the matrix has to be idempotent (it has to, because it is) we will use another approach. We note by [1, p.30,equation 2.57] and the previous analysis that is the least squares approximation in the space spanned by the columns of
is the least squares approximation in the space spanned by the columns of  to
to  . Applying the matrix
. Applying the matrix 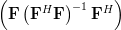 to
to  provides thus the least square approximation to
provides thus the least square approximation to  that is in the space spanned by the columns of
that is in the space spanned by the columns of  . But as
. But as  resides already within the space spanned by the columns of the matrix
resides already within the space spanned by the columns of the matrix  , the least square approximation that also resides in the same space has to be the vector
, the least square approximation that also resides in the same space has to be the vector  itself. But this simply means that consecutive applications of the same transform
provide the same result as the single application of the transform
itself. But this simply means that consecutive applications of the same transform
provide the same result as the single application of the transform 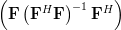 . Thus
. Thus 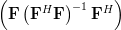 is idempotent. QED.
is idempotent. QED.
[1] Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”, Prentice Hall, ISBN: 0-13-598582-X.
[2] Lawrence J. Corwin and Robert H. Szczarba: “Calculus in Vector Spaces”, Marcel Dekker, Inc, 2nd edition, ISBN: 0824792793.
 is a full rank
is a full rank 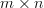 matrix with
matrix with 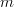 >
>  ,
,  is a
is a 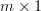 vector, and
vector, and  is an
is an 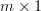 vector, that the effect of the linear transformation
vector, that the effect of the linear transformation
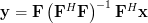 | (1) | ||
is to project
 onto the subspace spanned by the columns of
onto the subspace spanned by the columns of  . Specifically, if
. Specifically, if 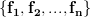 are the columns of
are the columns of  , the exercise [1, p. 34 exercise 2.4] asks to show that
, the exercise [1, p. 34 exercise 2.4] asks to show that
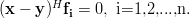 | (2) | ||
Furthermore it is asked why the transform
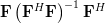 must be idempotent.
Solution: Let
must be idempotent.
Solution: Let 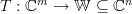 be the linear transform to which the matrix
be the linear transform to which the matrix 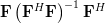 is associated to. We are asked to show that the linear transform is surjective (onto) to
is associated to. We are asked to show that the linear transform is surjective (onto) to 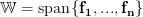 .
This linear transform can be thought as the composite of the linear transforms [2, p. 49, proposition 6.3]
.
This linear transform can be thought as the composite of the linear transforms [2, p. 49, proposition 6.3]
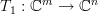 ,
,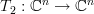 ,
,
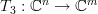 to which the matrices
to which the matrices 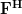 ,
,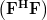 and
and  are associated respectively. We note that
are associated respectively. We note that 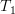 is surjective as the rank of the matrix equals
is surjective as the rank of the matrix equals  :
: 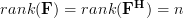 . Thus the whole image
. Thus the whole image 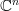 is spanned by this transform per definition. The transform
is spanned by this transform per definition. The transform 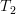 is bijective as an invertible matrix is associated with it. Therefore
is bijective as an invertible matrix is associated with it. Therefore 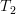 is also surjective to
is also surjective to 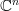 . From this we conclude that the standard basis
. From this we conclude that the standard basis 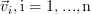 (
(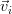 is the vector composed of zeros at all elements except the
is the vector composed of zeros at all elements except the 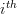 that is equal to one)
is also included in the image of
that is equal to one)
is also included in the image of 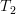 .
Because any vector
.
Because any vector 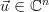 can be represented as a weighted sum of the standard basis:
can be represented as a weighted sum of the standard basis: 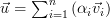 we obtain applying the linear transform
we obtain applying the linear transform 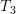 to this vector the following relation:
to this vector the following relation:
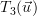 |  | 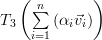 | |
 | 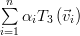 |
Now let
 be the matrix of the transform
be the matrix of the transform 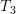 relative to the standard bases
relative to the standard bases 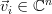 with
with 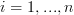 and
and 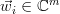 ,
, 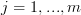 .
If the elements of the matrix are
.
If the elements of the matrix are 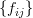 then the transform
then the transform 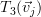 can be rewritten as [2, p. 47]:
can be rewritten as [2, p. 47]: 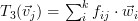 . This is simply the vector composed of the elements of the
. This is simply the vector composed of the elements of the 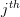 column of the matrix
column of the matrix  . This vector will be denoted as
. This vector will be denoted as 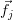 . Using matrix notation
. Using matrix notation 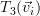 can be written simply as
can be written simply as 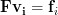 .
Thus
.
Thus 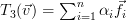 , which means that the image of
, which means that the image of 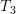 is composed of all linear combination of the columns of the corresponding matrix, this is per definition
is composed of all linear combination of the columns of the corresponding matrix, this is per definition 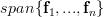 and thus the composite of the transforms
and thus the composite of the transforms 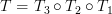 is surjective (onto) to
is surjective (onto) to 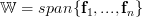 .
Now let us proceed to show that
.
Now let us proceed to show that
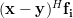 |  | 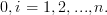 | (3) |
First we will compute the hermitian transpose of the column vector
 . By using the associative property of matrix multiplication and the rule [1, p. 23]
. By using the associative property of matrix multiplication and the rule [1, p. 23] 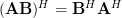 we derive the following relations:
we derive the following relations:
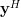 |  | 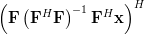 | |
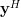 |  | 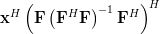 | |
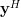 |  | ![\mathbf{x}^H \left(\left(\mathbf{F}^H\right)^H\left[\left(\mathbf{F}^H\mathbf{F}\right)^{-1}\right]^H\mathbf{F}^H\right)](https://lysario.de/wp-content/cache/tex_502f43684c5202a1ca8b21878daef6e4.png) | |
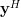 |  | 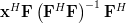 | (4) |
Now instead of multiplying
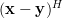 by one column
by one column 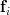 of the matrix
of the matrix ![\mathbf{F}=[\mathbf{f}_1 \cdots \mathbf{f}_i \cdots \mathbf{f}_n]](https://lysario.de/wp-content/cache/tex_6d210d4ed04bcea478b5e5437ecb3cdc.png) , as in (3),
we will proceed compute the multiplication with the whole matrix, effectiveley using all columns
, as in (3),
we will proceed compute the multiplication with the whole matrix, effectiveley using all columns 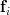 . Furthermore applying also (4) we obtain:
. Furthermore applying also (4) we obtain:
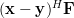 |  | 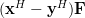 | |
 | 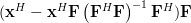 | ||
 | 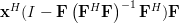 | ||
 | 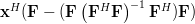 | ||
 | 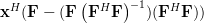 | ||
 | 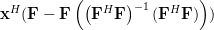 | ||
 | 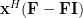 | ||
 | 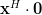 | ||
 | 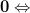 | ||
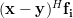 |  | 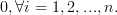 |
A matrix
 is idempotent by definition [1, p.21] when
is idempotent by definition [1, p.21] when 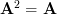 . Multiplying
. Multiplying 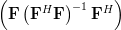 by itself and using again the associative property of matrix multiplication results in:
by itself and using again the associative property of matrix multiplication results in:
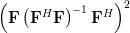 |  | 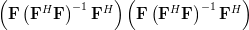 | |
 | 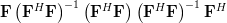 | ||
 | ![\mathbf{F}\left[\left(\mathbf{F}^H\mathbf{F}\right)^{-1}\left(\mathbf{F}^H\mathbf{F}\right)\right]\left(\mathbf{F}^H\mathbf{F}\right)^{-1}\mathbf{F}^H](https://lysario.de/wp-content/cache/tex_b4a58825ca0a89ca0647c2f3fba43d97.png) | ||
 | 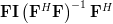 | ||
 | 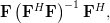 |
which proves that the matrix is idempotent. While this finding may be used to answer the question why the matrix has to be idempotent (it has to, because it is) we will use another approach. We note by [1, p.30,equation 2.57] and the previous analysis that
 is the least squares approximation in the space spanned by the columns of
is the least squares approximation in the space spanned by the columns of  to
to  . Applying the matrix
. Applying the matrix 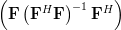 to
to  provides thus the least square approximation to
provides thus the least square approximation to  that is in the space spanned by the columns of
that is in the space spanned by the columns of  . But as
. But as  resides already within the space spanned by the columns of the matrix
resides already within the space spanned by the columns of the matrix  , the least square approximation that also resides in the same space has to be the vector
, the least square approximation that also resides in the same space has to be the vector  itself. But this simply means that consecutive applications of the same transform
provide the same result as the single application of the transform
itself. But this simply means that consecutive applications of the same transform
provide the same result as the single application of the transform 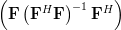 . Thus
. Thus 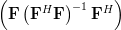 is idempotent. QED.
is idempotent. QED.[1] Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”, Prentice Hall, ISBN: 0-13-598582-X.
[2] Lawrence J. Corwin and Robert H. Szczarba: “Calculus in Vector Spaces”, Marcel Dekker, Inc, 2nd edition, ISBN: 0824792793.
Leave a reply