Lysario – by Panagiotis Chatzichrisafis
"ούτω γάρ ειδέναι το σύνθετον υπολαμβάνομεν, όταν ειδώμεν εκ τίνων και πόσων εστίν …"
Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”,p. 34 exercise 2.2
Author: Panagiotis21 Sep
In exercise [1, p. 34 exercise 2.2] we are asked to
prove that the rows and columns of a unitary matrix are orthonormal as per [1, p. 21,(2.21)].
Solution: A complex square matrix is unitary if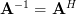 . Let
. Let 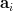 be the
be the 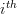 column vector of
column vector of  then
then
Computing the matrix product of the hermitian transpose and the matrix results in:
Thus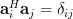 . QED.
. QED.
[1] Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”, Prentice Hall, ISBN: 0-13-598582-X.
Solution: A complex square matrix is unitary if
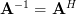 . Let
. Let 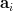 be the
be the 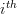 column vector of
column vector of  then
then
 |  | ![\left[ \begin{array}{*{20}c} \mathbf{a}_{1} & \mathbf{a}_{2} & \cdots & \mathbf{a}_{N} \\ \end{array} \right]](https://lysario.de/wp-content/cache/tex_4c9061614a1b16e844f5ec79ff59d8cd.png) | (1) |
Computing the matrix product of the hermitian transpose and the matrix results in:
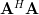 |  | ![\left[ \begin{array}{*{20}c} \mathbf{a}_1^H \\
\mathbf{a}_2^H \\ \vdots \\ \mathbf{a}_N^H \\ \end{array} \right] \left[ \begin{array}{*{20}c} \mathbf{a}_1 & \mathbf{a}_2 & \cdots & \mathbf{a}_N \\ \end{array} \right]](https://lysario.de/wp-content/cache/tex_693e3ed9724c6846fbefd325e00e0d92.png) | (2) |
 | ![\left[ \begin{array}{*{20}c} \mathbf{a}_1^H \mathbf{a}_1 & \mathbf{a}_1^H \mathbf{a}_2 & \cdots & \mathbf{a}_1^H \mathbf{a}_N \\ \mathbf{a}_2^H \mathbf{a}_1 & \mathbf{a}_2^H \mathbf{a}_2 & \cdots & \mathbf{a}_2^H \mathbf{a}_N \\ \vdots & \vdots & \vdots & \vdots \\
\mathbf{a}_N^H \mathbf{a}_1 & \mathbf{a}_N^H \mathbf{a}_2 & \cdots & \mathbf{a}_N^H \mathbf{a}_N \\ \end{array} \right]](https://lysario.de/wp-content/cache/tex_9b63cbc967d67e00638012dbeaf8b3ed.png) | (3) | |
 | 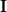 | (4) |
Thus
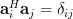 . QED.
. QED.[1] Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”, Prentice Hall, ISBN: 0-13-598582-X.
Leave a reply