Lysario – by Panagiotis Chatzichrisafis
"ούτω γάρ ειδέναι το σύνθετον υπολαμβάνομεν, όταν ειδώμεν εκ τίνων και πόσων εστίν …"
Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”,p. 34 exercise 2.1
Author: Panagiotis21 Sep
In exercise [1, p. 34 exercise 2.1] we are asked to prove that the inverse of a lower triangular matrix is also lower triangular by using relation [1, p. 23, (2.30)].
Solution: The determinant of a lower triangular matrix is given by [1, p. 20, (2.16)]
, as also by [1, p. 18, (2.1)]
In the previous equation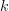 is any positive integer smaller or equal than the size
is any positive integer smaller or equal than the size  of the matrix. The element
of the matrix. The element 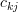 is given by
is given by 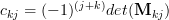 , where
, where 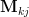 is the minor matrix obtained by removing the
is the minor matrix obtained by removing the 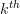 row and
row and 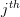 column from the matrix
column from the matrix 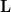 .
Now the elements
.
Now the elements 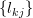 of the lower triangular matrix
of the lower triangular matrix 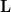 are zero
for
are zero
for 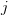 >
> 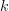 . Equation (2) can be rewritten for the lower triangular matrix as:
. Equation (2) can be rewritten for the lower triangular matrix as:
Using (1) and (3) we derive the following relations:
The left hand side of the previous equation equals zero because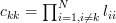 which can be derived by utilizing the fact that
which can be derived by utilizing the fact that 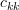 is the determinant of the lower triangular matrix that is obtained by
is the determinant of the lower triangular matrix that is obtained by 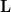 when the
when the 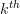 row and column are removed. Thus the following conditions must be satisfied, for all
row and column are removed. Thus the following conditions must be satisfied, for all 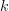 :
:
We note that the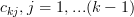 are independet of the
are independet of the 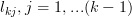 , because
, because 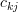 is obtained by
is obtained by 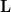 when the
when the 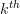 row is removed where the
row is removed where the 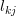 are located. It follows that the
are located. It follows that the 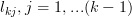 do not contribute to the result of
do not contribute to the result of 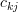 . But because the
. But because the 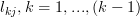 are not restricted to any values we derive the neccesity that
are not restricted to any values we derive the neccesity that
The matrix![\mathbf{C}=[c_{ij}]](https://lysario.de/wp-content/cache/tex_81d2da56ce54d6599d0c2f1a132b3a4d.png) is an upper triangular matrix as
is an upper triangular matrix as 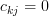 for
for 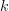 >
> 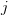 . The inverse of the lower triangular matrix is given by [1, p. 23, (2.30)]:
. The inverse of the lower triangular matrix is given by [1, p. 23, (2.30)]: 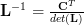 which is also a lower triangular matrix because
which is also a lower triangular matrix because 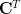 is lower triangular.
QED.
is lower triangular.
QED.
[1] Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”, Prentice Hall, ISBN: 0-13-598582-X.
Solution: The determinant of a lower triangular matrix is given by [1, p. 20, (2.16)]
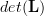 |  | 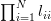 | (1) |
, as also by [1, p. 18, (2.1)]
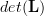 |  | 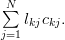 | (2) |
In the previous equation
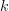 is any positive integer smaller or equal than the size
is any positive integer smaller or equal than the size  of the matrix. The element
of the matrix. The element 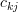 is given by
is given by 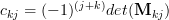 , where
, where 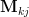 is the minor matrix obtained by removing the
is the minor matrix obtained by removing the 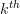 row and
row and 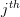 column from the matrix
column from the matrix 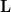 .
Now the elements
.
Now the elements 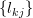 of the lower triangular matrix
of the lower triangular matrix 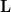 are zero
for
are zero
for 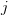 >
> 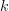 . Equation (2) can be rewritten for the lower triangular matrix as:
. Equation (2) can be rewritten for the lower triangular matrix as:
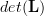 |  | 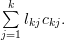 | (3) |
Using (1) and (3) we derive the following relations:
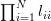 |  | 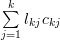 | (4) |
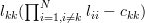 |  | 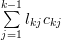 | (5) |
The left hand side of the previous equation equals zero because
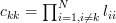 which can be derived by utilizing the fact that
which can be derived by utilizing the fact that 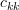 is the determinant of the lower triangular matrix that is obtained by
is the determinant of the lower triangular matrix that is obtained by 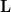 when the
when the 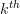 row and column are removed. Thus the following conditions must be satisfied, for all
row and column are removed. Thus the following conditions must be satisfied, for all 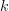 :
:
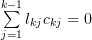 | (6) | ||
We note that the
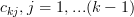 are independet of the
are independet of the 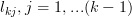 , because
, because 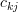 is obtained by
is obtained by 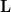 when the
when the 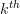 row is removed where the
row is removed where the 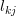 are located. It follows that the
are located. It follows that the 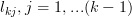 do not contribute to the result of
do not contribute to the result of 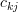 . But because the
. But because the 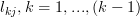 are not restricted to any values we derive the neccesity that
are not restricted to any values we derive the neccesity that
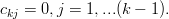 | (7) | ||
The matrix
![\mathbf{C}=[c_{ij}]](https://lysario.de/wp-content/cache/tex_81d2da56ce54d6599d0c2f1a132b3a4d.png) is an upper triangular matrix as
is an upper triangular matrix as 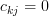 for
for 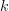 >
> 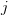 . The inverse of the lower triangular matrix is given by [1, p. 23, (2.30)]:
. The inverse of the lower triangular matrix is given by [1, p. 23, (2.30)]: 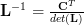 which is also a lower triangular matrix because
which is also a lower triangular matrix because 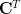 is lower triangular.
QED.
is lower triangular.
QED.[1] Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”, Prentice Hall, ISBN: 0-13-598582-X.
Leave a reply