Lysario – by Panagiotis Chatzichrisafis
"ούτω γάρ ειδέναι το σύνθετον υπολαμβάνομεν, όταν ειδώμεν εκ τίνων και πόσων εστίν …"
Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”,p. 34 exercise 2.7
Author: Panagiotis20 Nov
In exercise [1, p. 34 exercise 2.7] it is requested to find the inverse of the real symmetric Toeplitz matrix
and show that it is symmetric and persymmetric.
Solution: The cofactors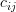 of the matrix
of the matrix  are given by:
are given by:
Thus the determinant of is given by (let
is given by (let 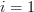 ):
):
The inverse of the matrix is thus equal to:
is thus equal to:
As it can be seen the matrix is persymmetric because the matrix elements![[\mathbf{A}^{-1}]_{ij}=m_{ij}](https://lysario.de/wp-content/cache/tex_d6f201e82428e084cea130921e250cc1.png) satisfy the relationship
satisfy the relationship 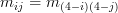 . It is also symmetric because
. It is also symmetric because 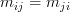 .
QED.
.
QED.
[1] Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”, Prentice Hall, ISBN: 0-13-598582-X.
![\mathbf{A} = \left[ {\begin{array}{*{20}c}
1 & { - a} & {a^2 } \\
{ - a} & 1 & { - a} \\
{a^2 } & { - a} & 1 \\
\end{array}} \right]](https://lysario.de/wp-content/cache/tex_7d981ef3134de2499a9848c900a503e7.png) | (1) | ||
and show that it is symmetric and persymmetric.
Solution: The cofactors
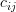 of the matrix
of the matrix  are given by:
are given by:
 |  | 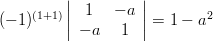 | |
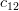 |  | 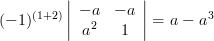 | |
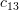 |  | 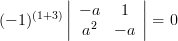 | |
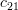 |  | 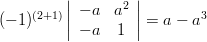 | |
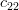 |  | 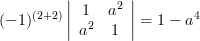 | |
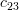 |  | 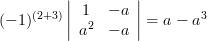 | |
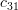 |  | 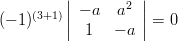 | |
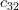 |  | 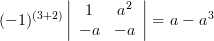 | |
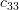 |  | 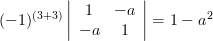 |
Thus the determinant of
 is given by (let
is given by (let 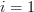 ):
):
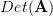 |  | 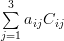 | |
 | 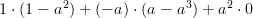 | ||
 | 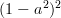 |
The inverse of the matrix
 is thus equal to:
is thus equal to:
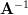 |  | ![\frac{1}{det{\mathbf{A}}}\left[ {\begin{array}{*{20}c}
c_{11} & c_{21} & c_{31} \\
c_{12} & c_{22} & c_{32} \\
c_{13} & c_{23} & c_{33} \\
\end{array}} \right]](https://lysario.de/wp-content/cache/tex_6a9f02f067084a7e0eec777c77bd84a0.png) | |
 | ![\frac{1}{(1-a^2)^2}\left[ {\begin{array}{*{20}c}
1-a^2 & a-a^3 & 0 \\
a-a^3 & 1-a^4 & a-a^3 \\
0 & a-a^3 & 1-a^2 \\
\end{array}} \right]](https://lysario.de/wp-content/cache/tex_5445fcda9b3586ed6b29283a37e53eb7.png) | ||
As it can be seen the matrix is persymmetric because the matrix elements
![[\mathbf{A}^{-1}]_{ij}=m_{ij}](https://lysario.de/wp-content/cache/tex_d6f201e82428e084cea130921e250cc1.png) satisfy the relationship
satisfy the relationship 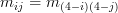 . It is also symmetric because
. It is also symmetric because 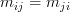 .
QED.
.
QED. [1] Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”, Prentice Hall, ISBN: 0-13-598582-X.
Leave a reply