Lysario – by Panagiotis Chatzichrisafis
"ούτω γάρ ειδέναι το σύνθετον υπολαμβάνομεν, όταν ειδώμεν εκ τίνων και πόσων εστίν …"
Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”,p. 34 exercise 2.6
Author: Panagiotis16 Nov
In problem [1, p. 34 exercise 2.6] we are asked to prove that if  and
and 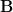 are complex
are complex 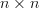 Hermitian matrices and
Hermitian matrices and 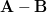 is positive semidefinite, then
is positive semidefinite, then ![\left[\mathbf{A}\right]_{ii} \geq \left[\mathbf{B}\right]_{ii}](https://lysario.de/wp-content/cache/tex_3652289cddad029917d54c1a0ed7c8cd.png) .
.
Solution: The key to the solution of this problem is provided by the theorem on [1, p. 26, 6.a.] which states: If a matrix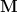 is positive definite (positive semidefinite),
is positive definite (positive semidefinite),
then a. the diagonal elements are positive (nonnegative). The diagonal elements of the matrix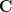 are
are ![\left[\mathbf{C}\right]_{ii}=\left[\mathbf{A}\right]_{ii}- \left[\mathbf{B}\right]_{ii}](https://lysario.de/wp-content/cache/tex_5b18f15abceb5d1122ddf0838a04bcdd.png) , thus:
, thus:
QED.
[1] Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”, Prentice Hall, ISBN: 0-13-598582-X.
 and
and 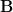 are complex
are complex 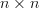 Hermitian matrices and
Hermitian matrices and 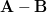 is positive semidefinite, then
is positive semidefinite, then ![\left[\mathbf{A}\right]_{ii} \geq \left[\mathbf{B}\right]_{ii}](https://lysario.de/wp-content/cache/tex_3652289cddad029917d54c1a0ed7c8cd.png) .
.
Solution: The key to the solution of this problem is provided by the theorem on [1, p. 26, 6.a.] which states: If a matrix
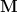 is positive definite (positive semidefinite),
is positive definite (positive semidefinite), then a. the diagonal elements are positive (nonnegative). The diagonal elements of the matrix
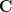 are
are ![\left[\mathbf{C}\right]_{ii}=\left[\mathbf{A}\right]_{ii}- \left[\mathbf{B}\right]_{ii}](https://lysario.de/wp-content/cache/tex_5b18f15abceb5d1122ddf0838a04bcdd.png) , thus:
, thus:
![\left[\mathbf{C}\right]_{ii} \geq 0](https://lysario.de/wp-content/cache/tex_dc6f1292faa427d1687099e71fe893e2.png) | (1) | ||
![\left[\mathbf{A}\right]_{ii}- \left[\mathbf{B}\right]_{ii} \geq 0](https://lysario.de/wp-content/cache/tex_e85c26a81002aebaa1665e37c0e7cde2.png) | (2) | ||
![\left[\mathbf{A}\right]_{ii} \geq \left[\mathbf{B}\right]_{ii}.](https://lysario.de/wp-content/cache/tex_c803b79cf06df511d9cb8d8574b8cda9.png) | (3) | ||
QED.
[1] Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”, Prentice Hall, ISBN: 0-13-598582-X.
Leave a reply