Lysario – by Panagiotis Chatzichrisafis
"ούτω γάρ ειδέναι το σύνθετον υπολαμβάνομεν, όταν ειδώμεν εκ τίνων και πόσων εστίν …"
Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”, p. 14 exercise 1.1
Author: Panagiotis2 Jan
Exercise [1, p. 14 exercise 1.1] asks to prove that
is a monotonically increasing function over the interval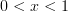 . Furthermore it asks to show that due to the monotonicity of the peaks of the spectral estimate shown in [1, Figure 1.2b] that they must also be present in the spectral estimate of [1, Figure 1.2a].
. Furthermore it asks to show that due to the monotonicity of the peaks of the spectral estimate shown in [1, Figure 1.2b] that they must also be present in the spectral estimate of [1, Figure 1.2a].
Solution: We notice that the first derivative of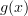 at any domain point
at any domain point  is positive
is positive 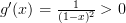


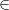
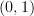 thus
thus 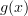 is a monotonically increasing function. For a function
is a monotonically increasing function. For a function 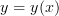 with range
with range 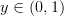 the extreme points (e.g.: maxima) of
the extreme points (e.g.: maxima) of 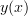 can be found on domain points where the first derivative is zero or at the boundaries. The function
can be found on domain points where the first derivative is zero or at the boundaries. The function 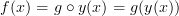 has a derivative equal to
has a derivative equal to
Thus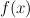 has the same local extrema as
has the same local extrema as 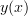 and peaks in
and peaks in 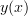 are shown as such in
are shown as such in 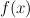 because rising sequences in
because rising sequences in 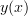 rise also in
rise also in 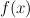 to higher values, and the first derivative of
to higher values, and the first derivative of 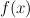 is zero at the same points where the derivative of
is zero at the same points where the derivative of 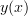 is zero; Q.E.D..
is zero; Q.E.D..
[1] Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”, Prentice Hall, ISBN: 0-13-598582-X.
 | (1) | ||
is a monotonically increasing function over the interval
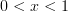 . Furthermore it asks to show that due to the monotonicity of the peaks of the spectral estimate shown in [1, Figure 1.2b] that they must also be present in the spectral estimate of [1, Figure 1.2a].
. Furthermore it asks to show that due to the monotonicity of the peaks of the spectral estimate shown in [1, Figure 1.2b] that they must also be present in the spectral estimate of [1, Figure 1.2a].
Solution: We notice that the first derivative of
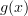 at any domain point
at any domain point  is positive
is positive 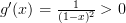


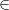
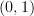 thus
thus 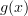 is a monotonically increasing function. For a function
is a monotonically increasing function. For a function 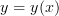 with range
with range 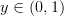 the extreme points (e.g.: maxima) of
the extreme points (e.g.: maxima) of 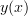 can be found on domain points where the first derivative is zero or at the boundaries. The function
can be found on domain points where the first derivative is zero or at the boundaries. The function 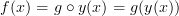 has a derivative equal to
has a derivative equal to
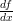 |  | 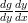 | |
 | 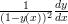 |
Thus
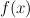 has the same local extrema as
has the same local extrema as 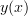 and peaks in
and peaks in 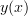 are shown as such in
are shown as such in 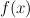 because rising sequences in
because rising sequences in 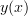 rise also in
rise also in 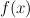 to higher values, and the first derivative of
to higher values, and the first derivative of 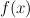 is zero at the same points where the derivative of
is zero at the same points where the derivative of 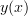 is zero; Q.E.D..
is zero; Q.E.D..[1] Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”, Prentice Hall, ISBN: 0-13-598582-X.
Leave a reply