Lysario – by Panagiotis Chatzichrisafis
"ούτω γάρ ειδέναι το σύνθετον υπολαμβάνομεν, όταν ειδώμεν εκ τίνων και πόσων εστίν …"
Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”,p. 62 exercise 3.15
Author: Panagiotis24 Mrz
In [1, p. 62 exercise 3.15] it is requested to verify the ACF and PSD relationships given in [1, p. 53 eq. (3.50)] and [1, p. 54 eq. (3.51)].
Solution: Starting from the first relationship of [1, p. 53 eq. (3.50)] and the definition of the cross correlation function we can derive
Using the starting assumption that![x[n]](https://lysario.de/wp-content/cache/tex_d3baaa3204e2a03ef9528a7d631a4806.png) is WSS we can derive the final result, that the cross correlation is also independent of the observation instance
is WSS we can derive the final result, that the cross correlation is also independent of the observation instance  and depends only on the lag
and depends only on the lag 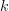 :
:
Similar the second relation can be obtained by:
and setting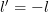 :
:
The third equation can be derived by:
By setting![\rho[k+l]=\sum_{\lambda} h[\lambda]r_{xx}[k+l-\lambda] =h[k+l]\ast r_{xx}[k+l]](https://lysario.de/wp-content/cache/tex_9097b96bda3e19c13c96ae1f2cc9e34a.png) we can rewrite (1) by
we can rewrite (1) by
which proves the last equation of [1, p. 53 eq. (3.50)] . We can now proceed to prove the relations for [1, p. 54 eq. (3.51)]
The second relation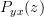 can similar be proven by:
can similar be proven by:
By change of variables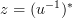 and
and 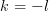 for the sum of the previous equation can be written as:
for the sum of the previous equation can be written as:
The last equation proves the second part of [1, p. 54 eq. (3.51)]. By similar reasoning the third relation can also be shown to be
which concludes the proof. QED.
[1] Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”, Prentice Hall, ISBN: 0-13-598582-X.
Solution: Starting from the first relationship of [1, p. 53 eq. (3.50)] and the definition of the cross correlation function we can derive
![r_{xy}[n,k]](https://lysario.de/wp-content/cache/tex_abefae1f0f9249ed88fb5ce51c3ed91f.png) |  | ![E\{x^{\ast}[n]y[n+k]\}](https://lysario.de/wp-content/cache/tex_3082153055e7fca5fa6f6417e4d5f0af.png) | |
 | ![E\{x^{\ast}[n]\sum\limits_{l}x[n+k-l]h[l]\}](https://lysario.de/wp-content/cache/tex_6e85a212b94a2574c1f583f4185244a7.png) | ||
 | ![\sum\limits_{l}E\{x^{\ast}[n]x[n+k-l]\}h[l]](https://lysario.de/wp-content/cache/tex_9626a98c9db075ca3541580d338bde74.png) |
Using the starting assumption that
![x[n]](https://lysario.de/wp-content/cache/tex_d3baaa3204e2a03ef9528a7d631a4806.png) is WSS we can derive the final result, that the cross correlation is also independent of the observation instance
is WSS we can derive the final result, that the cross correlation is also independent of the observation instance  and depends only on the lag
and depends only on the lag 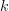 :
:
![r_{xy}[n,k]=r_{xy}[k]](https://lysario.de/wp-content/cache/tex_8fb90e3c85c1eaa32ffdd76132c262fa.png) |  | ![\sum\limits_{l}r_{xx}[k-l]h[l]](https://lysario.de/wp-content/cache/tex_01f33f02f2ed4578a1bb46df534a0ffc.png) |
Similar the second relation can be obtained by:
![r_{yx}[n,k]](https://lysario.de/wp-content/cache/tex_cf55c9c7c928a580ee81c65c50906292.png) |  | ![E\{y^{\ast}[n]x[n+k]\}](https://lysario.de/wp-content/cache/tex_adaa4627e5d263546f318a5386d251f5.png) | |
 | ![E\{\sum\limits_{l}x^{\ast}[n-l]h^{\ast}[l]x[n+k]\}](https://lysario.de/wp-content/cache/tex_0b0369a22a34b0ad02202d2ea00b0c58.png) | ||
 | ![\sum\limits_{l}E\{x^{\ast}[n-l]x[n+k]\}h^{\ast}[l]](https://lysario.de/wp-content/cache/tex_2ff8b162603160fff363e3a69dd1cf8c.png) | ||
 | ![\sum\limits_{l}r_{xx}[k+l]h^{\ast}[l]](https://lysario.de/wp-content/cache/tex_dff1052e8a01a16f8471a55512880b9f.png) |
and setting
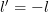 :
:
![r_{yx}[n,k]](https://lysario.de/wp-content/cache/tex_cf55c9c7c928a580ee81c65c50906292.png) |  | ![\sum\limits_{l^{\prime}}r_{xx}[k-l^{\prime}]h^{\ast}[-l^{\prime}]](https://lysario.de/wp-content/cache/tex_eb084d9b7818de8b387564bd100eb0f2.png) | |
 | ![r_{xx}[k]\star h^{\ast}[-k] =r_{yx}[k]](https://lysario.de/wp-content/cache/tex_f1d4e8367d03a4cfb4591ea32d429f17.png) | ||
The third equation can be derived by:
![r_{yy}[n,k]](https://lysario.de/wp-content/cache/tex_9f2aa1461b0e81ab067486a12235491e.png) |  | ![E\{y^{\ast}[n]y[n+k]\}](https://lysario.de/wp-content/cache/tex_0360d7e55b2d24eb8f0e48462ee52a2a.png) | |
 | ![E\{\sum\limits_{l}h^{\ast}[l]x^{\ast}[n-l]\sum\limits_{\lambda}h[\lambda]x[n+k-\lambda] \}](https://lysario.de/wp-content/cache/tex_15712b93166c2cbc248cefa13468bdb9.png) | ||
 | ![\sum\limits_{l}\sum\limits_{\lambda}h^{\ast}[l]h[\lambda]E\{x^{\ast}[n-l]x[n+k-\lambda] \}](https://lysario.de/wp-content/cache/tex_6071a811606feb690acfeec17b8a432c.png) | ||
 | ![\sum\limits_{l}h^{\ast}[l]\sum\limits_{\lambda} h[\lambda]r_{xx}[k+l-\lambda]](https://lysario.de/wp-content/cache/tex_b42d6cb51154c4ecbbd85bb5a5554bda.png) | (1) |
By setting
![\rho[k+l]=\sum_{\lambda} h[\lambda]r_{xx}[k+l-\lambda] =h[k+l]\ast r_{xx}[k+l]](https://lysario.de/wp-content/cache/tex_9097b96bda3e19c13c96ae1f2cc9e34a.png) we can rewrite (1) by
we can rewrite (1) by
![r_{yy}[n,k]](https://lysario.de/wp-content/cache/tex_9f2aa1461b0e81ab067486a12235491e.png) |  | ![\sum\limits_{l}h^{\ast}[l] \rho[k+l]](https://lysario.de/wp-content/cache/tex_caa927b002325abf140797615585be6f.png) | |
 | 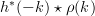 | ||
 | ![h^{\ast}(-k)\star h[k] \ast r_{xx}[k]](https://lysario.de/wp-content/cache/tex_f219a6b663b048787788506745301422.png) | (2) |
which proves the last equation of [1, p. 53 eq. (3.50)] . We can now proceed to prove the relations for [1, p. 54 eq. (3.51)]
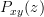 |  | ![\mathcal{Z}\{r_{xy}[k]\}](https://lysario.de/wp-content/cache/tex_8152596f1994935ac55dfcf085e49ae1.png) | |
 | ![\mathcal\{r_{xx}[k]\star h[k]\}](https://lysario.de/wp-content/cache/tex_fd99fe0c801673110b727500276aa9d7.png) | ||
 | 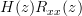 | (3) |
The second relation
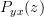 can similar be proven by:
can similar be proven by:
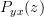 |  | ![\mathcal{Z}\{r_{yx}[k]\}](https://lysario.de/wp-content/cache/tex_a9c7124eecad9aacc7944610eed3b14c.png) | |
 | ![\mathcal{Z}\{h^{\ast}[-k]\star r_{xx}[k]\}](https://lysario.de/wp-content/cache/tex_90b7b76b8943ee163a520e6bb511af6d.png) | ||
 | ![\mathcal{Z}\{h^{\ast}[-k]\}R_{xx}(z)](https://lysario.de/wp-content/cache/tex_477139e4f021076e709754950f4a47b1.png) | ||
 | ![R_{xx}(z)\sum\limits_{k=-\infty}^{\infty}h^{\ast}[-k]z^{-k}](https://lysario.de/wp-content/cache/tex_8f936e0aaa7f8372f79db54739c856d2.png) |
By change of variables
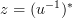 and
and 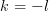 for the sum of the previous equation can be written as:
for the sum of the previous equation can be written as:
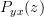 |  | ^{\ast}](https://lysario.de/wp-content/cache/tex_e66e3c6f8034aea743d148bfaa8a756f.png) | |
 | ![R_{xx}(z)(\sum\limits_{l=-\infty}^{\infty}h[l]u^{-l})^{\ast}](https://lysario.de/wp-content/cache/tex_b47995bafdccb55f9e4aaba0ba090105.png) | ||
 | 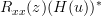 | ||
 | ![R_{xx}(z) \left[H(u=\frac{1}{z^{\ast}})\right]^{\ast}](https://lysario.de/wp-content/cache/tex_1be2b00074776e0395e2462cdc93421a.png) | ||
 | ![R_{xx}(z) \left[H(\frac{1}{z^{\ast}})\right]^{\ast}](https://lysario.de/wp-content/cache/tex_8611c5a2904ef5756c07fe653f209b6c.png) |
The last equation proves the second part of [1, p. 54 eq. (3.51)]. By similar reasoning the third relation can also be shown to be
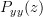 |  | ![\mathcal{Z}\{r_{yy}[k]\}](https://lysario.de/wp-content/cache/tex_0a8b5b2bb60b695552457af67494178a.png) | |
 | ![\mathcal{Z}\{h^{\ast}[-k]\star h[k]\star r_{xx}[k]\}](https://lysario.de/wp-content/cache/tex_1dd60956e92f46c5c44d16446e01a7d5.png) | ||
 | ![\mathcal{Z}\{h^{\ast}[-k]\}\mathcal{Z}\{ h[k]\}\mathcal{Z}\{r_{xx}[k]\}](https://lysario.de/wp-content/cache/tex_7bcf55f19773ce371e223d253264ebd1.png) | ||
 | ![\left[H(\frac{1}{z^{\ast}})\right]^{\ast}H(z)R_{xx}(z),](https://lysario.de/wp-content/cache/tex_7fe7ba39d93541f16b43202019b085c3.png) |
which concludes the proof. QED.
[1] Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”, Prentice Hall, ISBN: 0-13-598582-X.
Leave a reply