Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”,p. 62 exercise 3.13
Author: Panagiotis
23
Feb
In
[1, p. 62 exercise 3.13] it is requested to prove that the PSD of a real WSS random process is a real even function of frequency.
Solution:
The PSD of a WSS process is given by the Fourier transform of its autocorrelation function:
We note that for a real process
![x[n]](https://lysario.de/wp-content/cache/tex_d3baaa3204e2a03ef9528a7d631a4806.png)
,
![r_{xx}[k]](https://lysario.de/wp-content/cache/tex_86d1714abfafbac31f80e60727d3add6.png)
will be also real thus we obtain the relations:
First let us prove that for a real WSS this function is even. Having the previous relations in mind:
Let
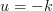
then
Thus we have shown that the PSD is symmetric
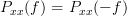
. The next step is to show that the PSD is also real. We know that the real part of a complex function is given as one half of the sum of the complex function with its complex conjugate form, that is
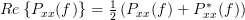
. Let’s determine the complex conjugate of the PSD:
Again relation (
2) was used in order to obtain the last result. The real part of the PSD is thus given by
because of (
4).
So the real part of the PSD
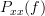
is the PSD itself, or stating it in another way: the PSD of a WSS process is real. Thus together with (
3) we have shown that the PSD of a real WSS random process is a real even function of frequency. QED.
[1] Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”, Prentice Hall, ISBN: 0-13-598582-X.
![x[n]](https://lysario.de/wp-content/cache/tex_d3baaa3204e2a03ef9528a7d631a4806.png) ,
, ![r_{xx}[k]](https://lysario.de/wp-content/cache/tex_86d1714abfafbac31f80e60727d3add6.png) will be also real thus we obtain the relations:
will be also real thus we obtain the relations:
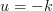 then
then
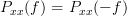 . The next step is to show that the PSD is also real. We know that the real part of a complex function is given as one half of the sum of the complex function with its complex conjugate form, that is
. The next step is to show that the PSD is also real. We know that the real part of a complex function is given as one half of the sum of the complex function with its complex conjugate form, that is 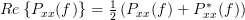 . Let’s determine the complex conjugate of the PSD:
. Let’s determine the complex conjugate of the PSD:
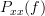 is the PSD itself, or stating it in another way: the PSD of a WSS process is real. Thus together with (3) we have shown that the PSD of a real WSS random process is a real even function of frequency. QED.
is the PSD itself, or stating it in another way: the PSD of a WSS process is real. Thus together with (3) we have shown that the PSD of a real WSS random process is a real even function of frequency. QED. ![P_{xx}(f)=\sum\limits_{k=-\infty}^{\infty}r_{xx}[k]e^{-j2\pi f k}.](https://lysario.de/wp-content/cache/tex_41a710fbcde77ee93a6413907722adb4.png)
![x[n]](https://lysario.de/wp-content/cache/tex_d3baaa3204e2a03ef9528a7d631a4806.png) ,
, ![r_{xx}[k]](https://lysario.de/wp-content/cache/tex_86d1714abfafbac31f80e60727d3add6.png) will be also real thus we obtain the relations:
will be also real thus we obtain the relations:
![r^{\ast}_{xx}[k]=r_{xx}[-k]=r_{xx}[k].](https://lysario.de/wp-content/cache/tex_3e32658d82d24dd7e3019908bb43eb6b.png)
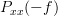

![\sum\limits_{k=-\infty}^{\infty}r_{xx}[k]e^{j2\pi f k}](https://lysario.de/wp-content/cache/tex_2c883b173702527903daabc95f0158ef.png)

![\sum\limits_{k=-\infty}^{\infty}r_{xx}[-k]e^{j2\pi f k}](https://lysario.de/wp-content/cache/tex_c1b393934220992a019c77d82ea5c3be.png)
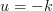 then
then
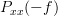

![\sum\limits_{u=-\infty}^{\infty}r_{xx}[u]e^{-j2\pi f u}](https://lysario.de/wp-content/cache/tex_de6c547795a70be6dd4117202d332def.png)

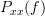
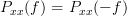 . The next step is to show that the PSD is also real. We know that the real part of a complex function is given as one half of the sum of the complex function with its complex conjugate form, that is
. The next step is to show that the PSD is also real. We know that the real part of a complex function is given as one half of the sum of the complex function with its complex conjugate form, that is 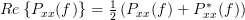 . Let’s determine the complex conjugate of the PSD:
. Let’s determine the complex conjugate of the PSD:
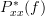

![\sum\limits_{k=-\infty}^{\infty}r^{\ast}_{xx}[k]e^{j2\pi f k}](https://lysario.de/wp-content/cache/tex_90126884baf279fbd80bcd8380ca03ea.png)

![\sum\limits_{k=-\infty}^{\infty}r_{xx}[-k]e^{j2\pi f k}=P_{xx}(-f)=P_{xx}(f)](https://lysario.de/wp-content/cache/tex_659077053ac333f376550a7bd09736cf.png)
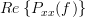

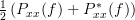

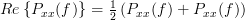

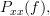
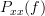 is the PSD itself, or stating it in another way: the PSD of a WSS process is real. Thus together with (3) we have shown that the PSD of a real WSS random process is a real even function of frequency. QED.
is the PSD itself, or stating it in another way: the PSD of a WSS process is real. Thus together with (3) we have shown that the PSD of a real WSS random process is a real even function of frequency. QED.
Leave a reply