Lysario – by Panagiotis Chatzichrisafis
"ούτω γάρ ειδέναι το σύνθετον υπολαμβάνομεν, όταν ειδώμεν εκ τίνων και πόσων εστίν …"
Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”,p. 34 exercise 2.9
Author: Panagiotis5 Jan
In [1, p. 34 exercise 2.9] we are asked to prove that the rank of the complex 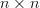 matrix
matrix
where the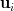 are linearly independent complex
are linearly independent complex 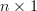 vectors and the
vectors and the 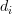 ‘s are real and positive, is equal to
‘s are real and positive, is equal to 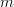 if
if 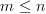 . Furthermore we are asked what the rank equals to if
. Furthermore we are asked what the rank equals to if 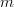 >
>  .
.
Solution:
Let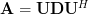 where
where ![{\bf U} = \left[ {\begin{array}{*{20}c} {{\bf u}_1 } & \cdots & {{\bf u}_m } \\ \end{array}} \right]](https://lysario.de/wp-content/cache/tex_65418a74374f858d31b0defab985a91c.png) and
and 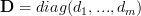 . If
. If 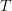 is the linear transform associated to
is the linear transform associated to  then
then 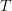 can be written as the composite of the linear transformations [2, propsition 6.3, p. 41]
can be written as the composite of the linear transformations [2, propsition 6.3, p. 41] 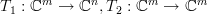 and
and 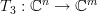 which are respectively associated to the matrices
which are respectively associated to the matrices 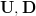 and
and 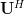 ,
, 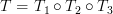 .
For
.
For 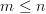 the
the 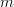 linear independent vectors span the subspace
linear independent vectors span the subspace 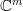 [2, proposition 4.3, page 112] thus the column rank of the matrix
[2, proposition 4.3, page 112] thus the column rank of the matrix 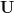 is
is 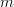 . The matrix
. The matrix 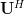 has the same rank as the matrix
has the same rank as the matrix 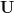 . The proof of this statement can be obtained by the observation that given
. The proof of this statement can be obtained by the observation that given 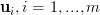 linear independent vectors, then the complex conjugates of those vectors are also linear independent. Thus
linear independent vectors, then the complex conjugates of those vectors are also linear independent. Thus ![{{\bf U}^{*}}^T = \left[ {\begin{array}{*{20}c} {{\bf u}^{*}_1 } & \cdots & {{\bf u}^{*}_m } \\ \end{array}} \right]^T](https://lysario.de/wp-content/cache/tex_47032866399116c845da7db20caf6860.png)
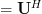 . Furthermore because the column rank equals the the row rank of a matrix [2, Theorem 4.4, page 218] we have
. Furthermore because the column rank equals the the row rank of a matrix [2, Theorem 4.4, page 218] we have 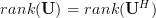 .
The linear transformation
.
The linear transformation 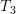 is surjective as its
is surjective as its 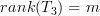 .
. 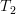 is bijective as the diagonal matrix associated with it is invertible [2, proposition 2.3, page 209]. The composite
is bijective as the diagonal matrix associated with it is invertible [2, proposition 2.3, page 209]. The composite 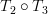 is thus surjective (onto) to
is thus surjective (onto) to 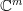 and thus the dimension of the image obtained by
and thus the dimension of the image obtained by 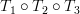 (per definition the rank of the matrix) is the same as the one that would be obtained by
(per definition the rank of the matrix) is the same as the one that would be obtained by 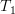 by linear combinations of a basis in
by linear combinations of a basis in 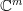 . Thus
. Thus 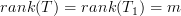 . QED.
For
. QED.
For 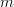 >
> 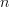 there can be no
there can be no 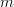 linear independent
linear independent 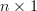 vectors. The maximum number of linear independent
vectors. The maximum number of linear independent 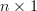 vectors is simply
vectors is simply  . This assertion can be proven by the equality of the row and column rank of a matrix.
For in this case the column rank of
. This assertion can be proven by the equality of the row and column rank of a matrix.
For in this case the column rank of 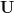 would be
would be 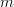 while the row rank of
while the row rank of 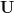 would not be larger than
would not be larger than  . The rank of the matrix cannot be larger than
. The rank of the matrix cannot be larger than  in this case.
in this case.
[1] Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”, Prentice Hall, ISBN: 0-13-598582-X.
[2] Lawrence J. Corwin and Robert H. Szczarba: “Calculus in Vector Spaces”, Marcel Dekker, Inc, 2nd edition, ISBN: 0824792793.
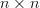 matrix
matrix
 | (1) | ||
where the
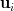 are linearly independent complex
are linearly independent complex 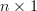 vectors and the
vectors and the 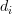 ‘s are real and positive, is equal to
‘s are real and positive, is equal to 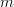 if
if 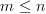 . Furthermore we are asked what the rank equals to if
. Furthermore we are asked what the rank equals to if 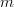 >
>  .
.
Solution:
Let
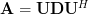 where
where ![{\bf U} = \left[ {\begin{array}{*{20}c} {{\bf u}_1 } & \cdots & {{\bf u}_m } \\ \end{array}} \right]](https://lysario.de/wp-content/cache/tex_65418a74374f858d31b0defab985a91c.png) and
and 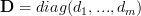 . If
. If 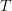 is the linear transform associated to
is the linear transform associated to  then
then 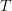 can be written as the composite of the linear transformations [2, propsition 6.3, p. 41]
can be written as the composite of the linear transformations [2, propsition 6.3, p. 41] 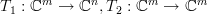 and
and 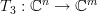 which are respectively associated to the matrices
which are respectively associated to the matrices 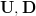 and
and 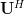 ,
, 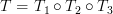 .
For
.
For 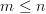 the
the 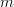 linear independent vectors span the subspace
linear independent vectors span the subspace 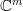 [2, proposition 4.3, page 112] thus the column rank of the matrix
[2, proposition 4.3, page 112] thus the column rank of the matrix 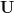 is
is 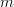 . The matrix
. The matrix 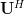 has the same rank as the matrix
has the same rank as the matrix 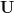 . The proof of this statement can be obtained by the observation that given
. The proof of this statement can be obtained by the observation that given 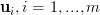 linear independent vectors, then the complex conjugates of those vectors are also linear independent. Thus
linear independent vectors, then the complex conjugates of those vectors are also linear independent. Thus ![{{\bf U}^{*}}^T = \left[ {\begin{array}{*{20}c} {{\bf u}^{*}_1 } & \cdots & {{\bf u}^{*}_m } \\ \end{array}} \right]^T](https://lysario.de/wp-content/cache/tex_47032866399116c845da7db20caf6860.png)
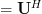 . Furthermore because the column rank equals the the row rank of a matrix [2, Theorem 4.4, page 218] we have
. Furthermore because the column rank equals the the row rank of a matrix [2, Theorem 4.4, page 218] we have 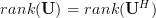 .
The linear transformation
.
The linear transformation 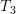 is surjective as its
is surjective as its 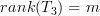 .
. 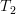 is bijective as the diagonal matrix associated with it is invertible [2, proposition 2.3, page 209]. The composite
is bijective as the diagonal matrix associated with it is invertible [2, proposition 2.3, page 209]. The composite 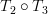 is thus surjective (onto) to
is thus surjective (onto) to 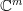 and thus the dimension of the image obtained by
and thus the dimension of the image obtained by 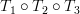 (per definition the rank of the matrix) is the same as the one that would be obtained by
(per definition the rank of the matrix) is the same as the one that would be obtained by 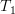 by linear combinations of a basis in
by linear combinations of a basis in 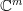 . Thus
. Thus 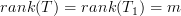 . QED.
For
. QED.
For 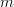 >
> 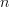 there can be no
there can be no 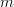 linear independent
linear independent 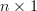 vectors. The maximum number of linear independent
vectors. The maximum number of linear independent 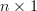 vectors is simply
vectors is simply  . This assertion can be proven by the equality of the row and column rank of a matrix.
For in this case the column rank of
. This assertion can be proven by the equality of the row and column rank of a matrix.
For in this case the column rank of 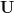 would be
would be 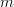 while the row rank of
while the row rank of 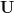 would not be larger than
would not be larger than  . The rank of the matrix cannot be larger than
. The rank of the matrix cannot be larger than  in this case.
in this case. [1] Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”, Prentice Hall, ISBN: 0-13-598582-X.
[2] Lawrence J. Corwin and Robert H. Szczarba: “Calculus in Vector Spaces”, Marcel Dekker, Inc, 2nd edition, ISBN: 0824792793.
Leave a reply