Lysario – by Panagiotis Chatzichrisafis
"ούτω γάρ ειδέναι το σύνθετον υπολαμβάνομεν, όταν ειδώμεν εκ τίνων και πόσων εστίν …"
Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”,p. 34 exercise 2.11
Author: Panagiotis24 Jan
In [1, p. 34 exercise 2.11] we are asked to find the eigenvalues of the circulant matrix given in [1, (2.27),p.22].
Solution: The matrix given in [1, (2.27),p.22] is
According to [1, (2.42),p.27] we can write the matrix as
with
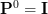 and where
and where 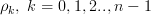 are the elements of the first row of the matrix
are the elements of the first row of the matrix 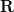 .
From the eigenvectors
.
From the eigenvectors 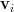 and eigenvalues
and eigenvalues 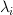 of
of 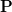 we can derive the eigenvalues of
we can derive the eigenvalues of 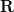 by:
by:
Thus the eigenvalues of the matrix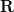 are given by
are given by 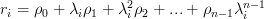 and are related to the eigenvectors
and are related to the eigenvectors ![\mathbf{v_i}=\frac{1}{\sqrt{n}} \left[ {\begin{array}{*{20}c}
1 & {e^{ - j\frac{{2\pi }}{n}(i - 1)} } & {e^{ - j\frac{{2\pi }}{n}2(i - 1)} } & \cdots & {e^{ - j\frac{{2\pi }}{n}(n - 1)(i - 1)} } \\
\end{array}} \right]^T](https://lysario.de/wp-content/cache/tex_1f405cf76d1d0320892ae84d0cfb4691.png) where
where 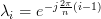 with
with 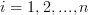 . The elements of the first row of the matrix
. The elements of the first row of the matrix 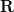 are
are 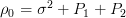 ,
, 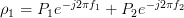 ,
, 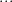 ,
, 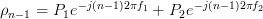 , as can be seen in the solution of [1, p. 34 exercise 2.5] given in [2, solution of exercise 2.5].
, as can be seen in the solution of [1, p. 34 exercise 2.5] given in [2, solution of exercise 2.5].
[1] Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”, Prentice Hall, ISBN: 0-13-598582-X.
[2] Panagiotis Chatzichrisafis: “Solution of exercise 2.5 from Kay’s Modern Spectral Estimation -Theory and Applications”, lysario.de.
Solution: The matrix given in [1, (2.27),p.22] is
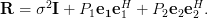 | (1) | ||
According to [1, (2.42),p.27] we can write the matrix as
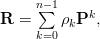 | (2) | ||
with
![\mathbf{P} = \left[ {\begin{array}{*{20}c}
0 & 1 & 0 & \cdots & 0 \\
0 & 0 & 1 & \cdots & 0 \\
\vdots & \vdots & \vdots & \vdots & \vdots \\
1 & 0 & 0 & \cdots & 0 \\
\end{array}} \right],](https://lysario.de/wp-content/cache/tex_36750e3b05d356bffcf6d4e9ca4ddd74.png) | (3) | ||
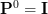 and where
and where 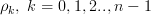 are the elements of the first row of the matrix
are the elements of the first row of the matrix 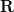 .
From the eigenvectors
.
From the eigenvectors 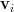 and eigenvalues
and eigenvalues 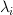 of
of 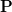 we can derive the eigenvalues of
we can derive the eigenvalues of 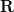 by:
by:
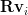 |  | 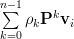 | |
 | 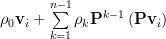 | ||
 | 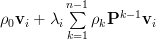 | ||
 | 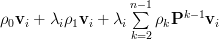 | ||
 | 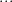 | ||
 | 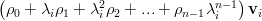 | (4) |
Thus the eigenvalues of the matrix
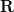 are given by
are given by 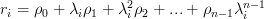 and are related to the eigenvectors
and are related to the eigenvectors ![\mathbf{v_i}=\frac{1}{\sqrt{n}} \left[ {\begin{array}{*{20}c}
1 & {e^{ - j\frac{{2\pi }}{n}(i - 1)} } & {e^{ - j\frac{{2\pi }}{n}2(i - 1)} } & \cdots & {e^{ - j\frac{{2\pi }}{n}(n - 1)(i - 1)} } \\
\end{array}} \right]^T](https://lysario.de/wp-content/cache/tex_1f405cf76d1d0320892ae84d0cfb4691.png) where
where 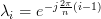 with
with 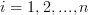 . The elements of the first row of the matrix
. The elements of the first row of the matrix 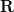 are
are 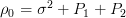 ,
, 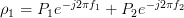 ,
, 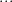 ,
, 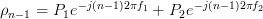 , as can be seen in the solution of [1, p. 34 exercise 2.5] given in [2, solution of exercise 2.5].
, as can be seen in the solution of [1, p. 34 exercise 2.5] given in [2, solution of exercise 2.5]. [1] Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”, Prentice Hall, ISBN: 0-13-598582-X.
[2] Panagiotis Chatzichrisafis: “Solution of exercise 2.5 from Kay’s Modern Spectral Estimation -Theory and Applications”, lysario.de.
Leave a reply