Lysario – by Panagiotis Chatzichrisafis
"ούτω γάρ ειδέναι το σύνθετον υπολαμβάνομεν, όταν ειδώμεν εκ τίνων και πόσων εστίν …"
Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”,p. 34 exercise 2.10
Author: Panagiotis7 Jan
In [1, p. 34 exercise 2.10] it is asked to prove that if  is a complex
is a complex 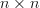 positive definite matrix and
positive definite matrix and 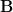 is a full rank complex
is a full rank complex 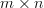 matrix with
matrix with 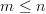 , then
, then 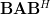 is also positive definite.
is also positive definite.
Solution:
Because the matrix is positive definite for any
is positive definite for any  :
:
In order to prove that the matrix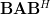 is also positive definite we have to show that
is also positive definite we have to show that  >
> 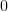 for any
for any  . Thus it is sufficient to show that
. Thus it is sufficient to show that  for any
for any  , because then due to (1) the positive defineteness of the matrix
, because then due to (1) the positive defineteness of the matrix  follows. Let
follows. Let  be the standard basis in
be the standard basis in 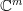 . Then any vector in
. Then any vector in 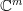 may be written as a linear combination of the standard base
may be written as a linear combination of the standard base  . Let
. Let  be the linear transformation associated to the matrix
be the linear transformation associated to the matrix  . Because
. Because  the dimension spanned by any transformed linear independent base will equal
the dimension spanned by any transformed linear independent base will equal 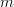 (definition of the rank of a matrix [2, p. 216]), thus
(definition of the rank of a matrix [2, p. 216]), thus  will be linear independent [2, propsition 4.3, p. 112] and the transform is injective which means that for
will be linear independent [2, propsition 4.3, p. 112] and the transform is injective which means that for  with
with  . The proof of this statement can be derived by the following reasoning:
. The proof of this statement can be derived by the following reasoning:
Relation (2) is obtained due to the linear independence of the vectors .
From this it follows that only the zero vector
.
From this it follows that only the zero vector  maps to
maps to  . Furthermore for any
. Furthermore for any 
 which proofs that the matrix
which proofs that the matrix 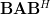 is positive definite. QED.
is positive definite. QED.
[1] Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”, Prentice Hall, ISBN: 0-13-598582-X.
[2] Lawrence J. Corwin and Robert H. Szczarba: “Calculus in Vector Spaces”, Marcel Dekker, Inc, 2nd edition, ISBN: 0824792793.
 is a complex
is a complex 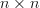 positive definite matrix and
positive definite matrix and 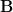 is a full rank complex
is a full rank complex 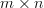 matrix with
matrix with 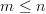 , then
, then 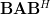 is also positive definite.
is also positive definite.
Solution:
Because the matrix
 is positive definite for any
is positive definite for any  :
:
 |  |  | (1) |
In order to prove that the matrix
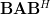 is also positive definite we have to show that
is also positive definite we have to show that  >
> 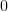 for any
for any  . Thus it is sufficient to show that
. Thus it is sufficient to show that  for any
for any  , because then due to (1) the positive defineteness of the matrix
, because then due to (1) the positive defineteness of the matrix  follows. Let
follows. Let  be the standard basis in
be the standard basis in 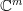 . Then any vector in
. Then any vector in 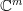 may be written as a linear combination of the standard base
may be written as a linear combination of the standard base  . Let
. Let  be the linear transformation associated to the matrix
be the linear transformation associated to the matrix  . Because
. Because  the dimension spanned by any transformed linear independent base will equal
the dimension spanned by any transformed linear independent base will equal 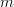 (definition of the rank of a matrix [2, p. 216]), thus
(definition of the rank of a matrix [2, p. 216]), thus  will be linear independent [2, propsition 4.3, p. 112] and the transform is injective which means that for
will be linear independent [2, propsition 4.3, p. 112] and the transform is injective which means that for  with
with  . The proof of this statement can be derived by the following reasoning:
. The proof of this statement can be derived by the following reasoning:
 |  |  | |
 |  |  | |
 |  |  | |
 |  |  | |
 |  |  | (2) |
 |  |  |
Relation (2) is obtained due to the linear independence of the vectors
 .
From this it follows that only the zero vector
.
From this it follows that only the zero vector  maps to
maps to  . Furthermore for any
. Furthermore for any 
 which proofs that the matrix
which proofs that the matrix 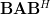 is positive definite. QED.
is positive definite. QED.[1] Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”, Prentice Hall, ISBN: 0-13-598582-X.
[2] Lawrence J. Corwin and Robert H. Szczarba: “Calculus in Vector Spaces”, Marcel Dekker, Inc, 2nd edition, ISBN: 0824792793.
Leave a reply