Lysario – by Panagiotis Chatzichrisafis
"ούτω γάρ ειδέναι το σύνθετον υπολαμβάνομεν, όταν ειδώμεν εκ τίνων και πόσων εστίν …"
Liboff: “Introductory Quantum Mechanics”, 2nd edition p.86 exercise 3.16
Author: Panagiotis2 Jan
The exercise [1, p. 86 ex. 3.16] asks to prove that if the eigenfunctions and eigenvalues of an operator 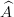 are
are 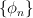 and
and 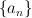 , respectively (
, respectively (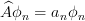 ) then the eigenfunctions of a function
) then the eigenfunctions of a function 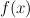 having an expansion of the form:
having an expansion of the form:
will also be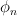 with corresponding eigenvalues
with corresponding eigenvalues 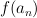 ,
, 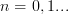 . That is
. That is 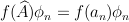 .
.
Solution:To prove this feature, one must have the distributive property of operators in mind which can be stated as: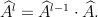 Iterative application of the operator
Iterative application of the operator 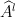 to the eigenfunction
to the eigenfunction 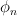 gives the following result:
gives the following result:
The function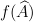 can be written with the use of the given expansion as:
can be written with the use of the given expansion as:
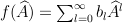 Applying the right hand side to an eigenfunction
Applying the right hand side to an eigenfunction 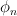 results in:
results in:
The last result (3) means that the eigenfunctions of an operator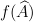 are the same as for the operator
are the same as for the operator 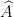 but the eigenvalues are given by
but the eigenvalues are given by 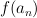 where
where 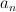 are the eigenvalues of the operator
are the eigenvalues of the operator 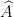 ; Q.E.D..
; Q.E.D..
[1] Richard L. Liboff: “Introductory Quantum Mechanics”, 2nd edition, ISBN: 0-201-54715-5.
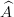 are
are 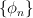 and
and 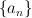 , respectively (
, respectively (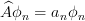 ) then the eigenfunctions of a function
) then the eigenfunctions of a function 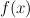 having an expansion of the form:
having an expansion of the form:
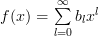 | (1) | ||
will also be
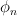 with corresponding eigenvalues
with corresponding eigenvalues 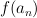 ,
, 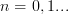 . That is
. That is 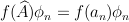 .
.
Solution:To prove this feature, one must have the distributive property of operators in mind which can be stated as:
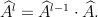 Iterative application of the operator
Iterative application of the operator 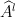 to the eigenfunction
to the eigenfunction 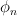 gives the following result:
gives the following result:
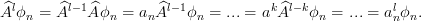 | (2) | ||
The function
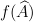 can be written with the use of the given expansion as:
can be written with the use of the given expansion as:
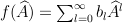 Applying the right hand side to an eigenfunction
Applying the right hand side to an eigenfunction 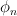 results in:
results in:
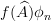 |  | 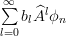 | |
 | 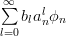 | ||
 | 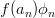 | (3) |
The last result (3) means that the eigenfunctions of an operator
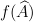 are the same as for the operator
are the same as for the operator 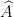 but the eigenvalues are given by
but the eigenvalues are given by 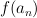 where
where 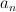 are the eigenvalues of the operator
are the eigenvalues of the operator 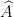 ; Q.E.D..
; Q.E.D..[1] Richard L. Liboff: “Introductory Quantum Mechanics”, 2nd edition, ISBN: 0-201-54715-5.
Leave a reply