Lysario – by Panagiotis Chatzichrisafis
"ούτω γάρ ειδέναι το σύνθετον υπολαμβάνομεν, όταν ειδώμεν εκ τίνων και πόσων εστίν …"
Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”,p. 62 exercise 3.17
Author: Panagiotis19 Apr
In [1, p. 62 exercise 3.17] we are asked to verify that the variance of the sample mean estimator for the mean of a real WSS random process
is given by [1, eq. (3.60), p. 58]. For the case when![x[n]](https://lysario.de/wp-content/cache/tex_d3baaa3204e2a03ef9528a7d631a4806.png) is real white noise we are asked to what the variance expression does reduce to.
A hint that is given is to use the relationship from [1, eq. (3.64), p. 59].
is real white noise we are asked to what the variance expression does reduce to.
A hint that is given is to use the relationship from [1, eq. (3.64), p. 59].
Solution: Let’s reproduce the corresponding equations cited in the problem statement, so [1, eq. (3.60), p. 58] is given by
while [1, eq. (3.64), p. 59] is given by:
First we note that the mean of the sample mean converges to the true mean of the WSS random process![x[n]](https://lysario.de/wp-content/cache/tex_d3baaa3204e2a03ef9528a7d631a4806.png) :
:
From this we can derive the variance of the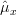 as:
as:
The squared sample mean can be written as:
From the previous relation we can derive that the mean squared sample mean is given by:
In the previous relations the factors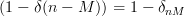 and
and 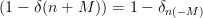 denote that for
denote that for 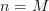 the second summand, while for
the second summand, while for 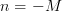 the third summand degenerates to zero.
The three double sums can be further simplified:
the third summand degenerates to zero.
The three double sums can be further simplified:
The second double sum can be written by:
while similar to the previous derivation the third double sum can be simplified to:
Using (3),(4) and (5) in (2) we derive the relationship:
Observe that we could have replaced in (1) the sum![\sum_{k=-M-n}^{M-n}r_{xx}[k]](https://lysario.de/wp-content/cache/tex_6a637b736fb66c3b0eadc5bf548acef2.png) by its equivalent form
by its equivalent form ![\sum_{k=-M}^{M}r_{xx}[k-n]](https://lysario.de/wp-content/cache/tex_3f5b522e59c60cd506578271c6d3c1f9.png) and applied relation [1, eq. (3.64), p. 59] of the hint. Then we would have come to the same result. In the approach taken in this solution we also derived the relation provided by the hint.
Now relating the autocovariance to the autocorrelation function:
and applied relation [1, eq. (3.64), p. 59] of the hint. Then we would have come to the same result. In the approach taken in this solution we also derived the relation provided by the hint.
Now relating the autocovariance to the autocorrelation function:
and replacing the autocorrelation in (6) by![r_{xx}[k]=c_{xx}[k]+\mu_{x}^{2}](https://lysario.de/wp-content/cache/tex_df64c393064cb5c4f3055c9655b56073.png) we obtain the variance of the sample mean as:
we obtain the variance of the sample mean as:
Noting that [2, p. 125]: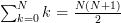 we can simplify the second part of the previous equation by:
we can simplify the second part of the previous equation by:
So finally we can rewrite the variance of the sample (7) mean as :
which is the relation of the sample mean used in [1, eq. (3.60), p. 58]. QED.
[1] Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”, Prentice Hall, ISBN: 0-13-598582-X.
[2] Granino A. Korn and Theresa M. Korn: “Mathematical Handbook for Scientists and Engineers”, Dover, ISBN: 978-0-486-41147-7.
![\frac{1}{2M+1}\sum\limits_{n=-M}^{n=M}x[n]](https://lysario.de/wp-content/cache/tex_1802f56fef4f03089a8b530f29ffae10.png) | |||
is given by [1, eq. (3.60), p. 58]. For the case when
![x[n]](https://lysario.de/wp-content/cache/tex_d3baaa3204e2a03ef9528a7d631a4806.png) is real white noise we are asked to what the variance expression does reduce to.
A hint that is given is to use the relationship from [1, eq. (3.64), p. 59].
is real white noise we are asked to what the variance expression does reduce to.
A hint that is given is to use the relationship from [1, eq. (3.64), p. 59].
Solution: Let’s reproduce the corresponding equations cited in the problem statement, so [1, eq. (3.60), p. 58] is given by
![\lim\limits_{M\rightarrow \infty}\frac{1}{2M+1} \sum\limits_{k=-2M}^{2M}\left(1-\frac{|k|}{2M+1}\right)c_{xx}[k]=0.](https://lysario.de/wp-content/cache/tex_0b499c889ff801e3e4cfe1eb020d2cc6.png) | |||
while [1, eq. (3.64), p. 59] is given by:
![\sum\limits_{m=-M}^{M}\sum\limits_{n=-M}^{M}g[m-n]=\sum\limits_{k=-2M}^{2M} \left(2M+1-|k|\right)g[k]](https://lysario.de/wp-content/cache/tex_e252ca41cef09873b0fe68f74a0a3cbb.png) | |||
First we note that the mean of the sample mean converges to the true mean of the WSS random process
![x[n]](https://lysario.de/wp-content/cache/tex_d3baaa3204e2a03ef9528a7d631a4806.png) :
:
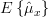 |  | ![\frac{1}{2M+1}\sum\limits_{n=-M}^{M} E\left\{ x[n]\right\}](https://lysario.de/wp-content/cache/tex_f6bd9c48c4d56674f504638e16edb6c6.png) | |
 | 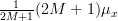 | ||
 | 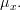 |
From this we can derive the variance of the
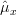 as:
as:
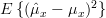 |  | 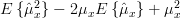 | |
 | 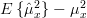 | ||
The squared sample mean can be written as:
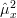 |  | ![\left(\frac{1}{2M+1}\right)^{2} \sum\limits_{n=-M}^{n=M} x[n] \sum\limits_{l=-M}^{l=M}x[l]](https://lysario.de/wp-content/cache/tex_ca3e0ddb764d6a3c9097a1432b47b7d3.png) | |
 | ![\left(\frac{1}{2M+1}\right)^{2}\sum\limits_{n=-M}^{n=M}\sum\limits_{l=-M}^{l=M}x[n]x[l], \; \textnormal{replacing } l=n+k \Rightarrow](https://lysario.de/wp-content/cache/tex_d971b37c82939f61543d9d5801d45e5b.png) | ||
 | ![\left(\frac{1}{2M+1}\right)^{2}\sum\limits_{n=-M}^{n=M}\sum\limits_{k=-M-n}^{k=M-n}x[n]x[n+k].](https://lysario.de/wp-content/cache/tex_524140ec37a2340a41b30b949aac8bf2.png) |
From the previous relation we can derive that the mean squared sample mean is given by:
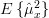 |  | ![\left(\frac{1}{2M+1}\right)^{2}\sum\limits_{n=-M}^{n=M}\sum\limits_{k=-M-n}^{k=M-n}\ensuremath{E\left\{x[n]x[n+k]\right\}}](https://lysario.de/wp-content/cache/tex_317ff3a81fbf73676bcc6860ce3ca115.png) | |
 | ![\left(\frac{1}{2M+1}\right)^{2}\sum\limits_{n=-M}^{n=M}\sum\limits_{k=-M-n}^{k=M-n}r_{xx}[k]](https://lysario.de/wp-content/cache/tex_1f50033434ff7d80f9c93940bed3b407.png) | (1) | |
 | ![\left(\frac{1}{2M+1}\right)^{2}\sum\limits_{n=-M}^{n=M}\sum\limits_{k=-2M}^{2M}r_{xx}[k]](https://lysario.de/wp-content/cache/tex_199ece4161bcb7662515f993c1ca24a5.png) | ||
 | ![- \left(\frac{1}{2M+1}\right)^{2}\sum\limits_{n=-M}^{n=M}(1-\delta(n-M))\sum\limits_{k=-2M}^{-M-n-1}r_{xx}[k]](https://lysario.de/wp-content/cache/tex_3209dd09953589843c62c97d7baa3911.png) | ||
 | ![- \left(\frac{1}{2M+1}\right)^{2}\sum\limits_{n=-M}^{n=M}(1-\delta(n+M))\sum\limits_{k=M-n+1}^{2M}r_{xx}[k]](https://lysario.de/wp-content/cache/tex_3c579113779788f576074a579b80514e.png) | (2) |
In the previous relations the factors
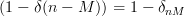 and
and 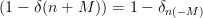 denote that for
denote that for 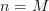 the second summand, while for
the second summand, while for 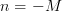 the third summand degenerates to zero.
The three double sums can be further simplified:
the third summand degenerates to zero.
The three double sums can be further simplified:
![\sum\limits_{n=-M}^{n=M}\sum\limits_{k=-2M}^{2M}r_{xx}[k] =(2M+1)\sum\limits_{k=-2M}^{2M}r_{xx}[k].](https://lysario.de/wp-content/cache/tex_de180dd0158180fe708e9aa11872d161.png) | (3) | ||
The second double sum can be written by:
![(1-\delta_{nM})\sum\limits_{n=-M}^{M}\sum\limits_{k=-2M}^{-M-n-1}r_{xx}[k]](https://lysario.de/wp-content/cache/tex_b5ba37e14cc35676ccfaa1c6d203399e.png) |  | ![\underbrace{0}_{n=M}+\underbrace{r_{xx}[-2M]}_{n=M-1} +](https://lysario.de/wp-content/cache/tex_4a33f504d780a2ddfebc0ac04bc949d6.png) | |
 | ![+\underbrace{r_{xx}[-2M]+r_{xx}[-2M+1]}_{n=M-2}](https://lysario.de/wp-content/cache/tex_c42a8ecbeb8ef251cdc4173a20d909ad.png) | ||
 | ![+...+\underbrace{\sum\limits_{k=-2M}^{-1}r_{xx}[k]}_{n=-M}](https://lysario.de/wp-content/cache/tex_9efc22c952d8ba18f0f1d7a3e10741b3.png) | ||
 | ![2M r_{xx}[-2M] +](https://lysario.de/wp-content/cache/tex_b3fe520c1fec030c5fb82812c9152ab1.png) | ||
 | ![+ (2M-1) r_{xx}[-2M+1] +](https://lysario.de/wp-content/cache/tex_ef55e8b0feec659d86412a1551750fe0.png) | ||
 | ![+ ... + r_{xx}[-1]](https://lysario.de/wp-content/cache/tex_2a6ddcd33c2ec41d3961fa19b81d3d1b.png) | ||
 | ![\sum\limits_{u=-2M}^{0} |u|r_{xx}[u],](https://lysario.de/wp-content/cache/tex_3c3bf44215e7f043c48984b18514ca43.png) | (4) |
while similar to the previous derivation the third double sum can be simplified to:
![(1-\delta_{n(-M)})\sum\limits_{n=-M}^{M}\sum\limits_{k=-2M}^{-M-n-1}r_{xx}[k]](https://lysario.de/wp-content/cache/tex_0e7da7f7d8383cd538a8c4d55aa38b7d.png) |  | ![\underbrace{0}_{n=-M}+\underbrace{r_{xx}[-2M]}_{n=-M+1} +](https://lysario.de/wp-content/cache/tex_c04a93614a798ab765890b2f6da0aea7.png) | |
 | ![+\underbrace{r_{xx}[-2M]+r_{xx}[-2M+1]}_{n=-M+2}](https://lysario.de/wp-content/cache/tex_d37c169cbfee62c2f0408837cc7a8c88.png) | ||
 | ![+...+\underbrace{\sum\limits_{k=1}^{2M}r_{xx}[k]}_{n=M}](https://lysario.de/wp-content/cache/tex_6d68dbbc5d985140e199b177c88782a9.png) | ||
 | ![2M r_{xx}[2M]](https://lysario.de/wp-content/cache/tex_07709c02aa6fdbc02fd77154fb10e5ae.png) | ||
 | ![+(2M-1) r_{xx}[2M-1]](https://lysario.de/wp-content/cache/tex_aa5fb06576916ff6ed70852e7625adad.png) | ||
 | ![+ ... + r_{xx}[1]](https://lysario.de/wp-content/cache/tex_2e495564a0f6a3f00c442225e0e958b8.png) | ||
 | ![\sum\limits_{u=0}^{2M} |u|r_{xx}[u],](https://lysario.de/wp-content/cache/tex_3b041e4aa32b3a552c7ac74e8dcc392c.png) | (5) |
Using (3),(4) and (5) in (2) we derive the relationship:
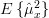 |  | ![\left(\frac{1}{2M+1}\right)\sum\limits_{k=-2M}^{2M}r_{xx}[k]](https://lysario.de/wp-content/cache/tex_967a7b3547edaa3815d92924db58f948.png) | |
 | ![-\left(\frac{1}{2M+1}\right)^{2} \left(\sum\limits_{u=-2M}^{0} |u|r_{xx}[u]+\sum\limits_{u=0}^{2M} |u|r_{xx}[u]\right)](https://lysario.de/wp-content/cache/tex_1bbf4430e01236349b29d7b91ebdbbab.png) | ||
 | ![\left(\frac{1}{2M+1}\right)\sum\limits_{k=-2M}^{2M}r_{xx}[k] -\left(\frac{1}{2M+1}\right)^{2} \sum\limits_{u=-2M}^{2M} |u|r_{xx}[u]](https://lysario.de/wp-content/cache/tex_8f3d9b1dfb237857f98c171926bbe659.png) | ||
 | ![\frac{1}{2M+1} \sum\limits_{k=-2M}^{2M}\left(1-\frac{1}{2M+1}|k|\right)r_{xx}[k]](https://lysario.de/wp-content/cache/tex_8d2f90d7c42d4b0cffd2c702a17f4a97.png) | (6) |
Observe that we could have replaced in (1) the sum
![\sum_{k=-M-n}^{M-n}r_{xx}[k]](https://lysario.de/wp-content/cache/tex_6a637b736fb66c3b0eadc5bf548acef2.png) by its equivalent form
by its equivalent form ![\sum_{k=-M}^{M}r_{xx}[k-n]](https://lysario.de/wp-content/cache/tex_3f5b522e59c60cd506578271c6d3c1f9.png) and applied relation [1, eq. (3.64), p. 59] of the hint. Then we would have come to the same result. In the approach taken in this solution we also derived the relation provided by the hint.
Now relating the autocovariance to the autocorrelation function:
and applied relation [1, eq. (3.64), p. 59] of the hint. Then we would have come to the same result. In the approach taken in this solution we also derived the relation provided by the hint.
Now relating the autocovariance to the autocorrelation function:
![c_{xx}[k]](https://lysario.de/wp-content/cache/tex_be7c8f1bd829ab6d117b7a827ab99d91.png) |  | ![E\left\{(x[n]-\mu_{x})(x[n+k]-\mu_{x})\right\}](https://lysario.de/wp-content/cache/tex_23cf961d22540c3ae331aad2cd2a439f.png) | |
 | ![\ensuremath{E\left\{x[n]x[n+k]\right\}}-\ensuremath{E\left\{x[n]\right\}}\mu_{x}-\mu_{x}\ensuremath{E\left\{x[n+k]\right\}}+\mu_{x}^{2}](https://lysario.de/wp-content/cache/tex_470c3a6b3ff20865fb940fc06cee07db.png) | ||
 | ![r_{xx}[k]-\mu_{x}^{2}](https://lysario.de/wp-content/cache/tex_d73a97a1a82050231e1c3ed02af674e0.png) |
and replacing the autocorrelation in (6) by
![r_{xx}[k]=c_{xx}[k]+\mu_{x}^{2}](https://lysario.de/wp-content/cache/tex_df64c393064cb5c4f3055c9655b56073.png) we obtain the variance of the sample mean as:
we obtain the variance of the sample mean as:
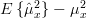 |  | ![\frac{1}{2M+1}\sum\limits_{k=-2M}^{2M}\left(1-\frac{|k|}{2M+1}\right)(c_{xx}[k]+\mu_{x}^{2}) - \mu_{x}^{2}](https://lysario.de/wp-content/cache/tex_f77d0ff6751906e26c2d2c77c26b1722.png) | |
 | ![\frac{1}{2M+1}\sum\limits_{k=-2M}^{k=2M}\left(1-\frac{|k|}{2M+1}\right)c_{xx}[k]](https://lysario.de/wp-content/cache/tex_9aba1dc9147fcf40537b965cd62a66dd.png) | ||
 | 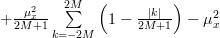 | (7) |
Noting that [2, p. 125]:
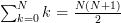 we can simplify the second part of the previous equation by:
we can simplify the second part of the previous equation by:
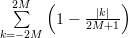 |  | 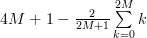 | |
 | 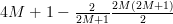 | ||
 | 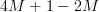 | ||
 | 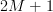 | (8) |
So finally we can rewrite the variance of the sample (7) mean as :
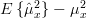 |  | ![\frac{1}{2M+1}\sum\limits_{k=-2M}^{k=2M}\left(1-\frac{|k|}{2M+1}\right)c_{xx}[k]](https://lysario.de/wp-content/cache/tex_d7a30028ac4ed6db6d87fb92eb2a4a14.png) | |
 | 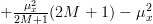 | ||
 | ![\frac{1}{2M+1}\sum\limits_{k=-2M}^{k=2M}\left(1-\frac{|k|}{2M+1}\right)c_{xx}[k]](https://lysario.de/wp-content/cache/tex_d7a30028ac4ed6db6d87fb92eb2a4a14.png) | (9) |
which is the relation of the sample mean used in [1, eq. (3.60), p. 58]. QED.
[1] Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”, Prentice Hall, ISBN: 0-13-598582-X.
[2] Granino A. Korn and Theresa M. Korn: “Mathematical Handbook for Scientists and Engineers”, Dover, ISBN: 978-0-486-41147-7.
Leave a reply