Lysario – by Panagiotis Chatzichrisafis
"ούτω γάρ ειδέναι το σύνθετον υπολαμβάνομεν, όταν ειδώμεν εκ τίνων και πόσων εστίν …"
Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”,p. 35 exercise 2.14
Author: Panagiotis28 Mai
In [1, p. 35 exercise 2.14] we are asked to consider the solution to the set of linear equations
where is a
is a 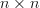 hermitian matrix given by:
hermitian matrix given by:
and is a complex
is a complex 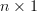 vector given by
vector given by
The complex vectors are defined in [1, p.22, (2.27)]. Furthermore we are asked to assumed that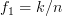 ,
, 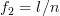 for
for 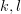 are distinct integers in the range
are distinct integers in the range ![[-n/2,n/2-1]](https://lysario.de/wp-content/cache/tex_24916734a0a5230271c84429761581eb.png) for
for  even and
even and ![[-(n-1)/2,(n-1)/2]](https://lysario.de/wp-content/cache/tex_b9ee4eee41d27a8e5eea256f738e00e2.png) for
for  odd.
odd.  is defined to be a
is defined to be a 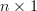 vector.
It is requested to show that
vector.
It is requested to show that  is a singular matrix (assuming
is a singular matrix (assuming 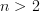 ) and that there are infinite number of solutions.
A further task is to find the general solution and also the minimum norm solution of the set of linear equations. The hint provided by the exercise is to note that
) and that there are infinite number of solutions.
A further task is to find the general solution and also the minimum norm solution of the set of linear equations. The hint provided by the exercise is to note that 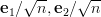 are eigenvectors of
are eigenvectors of  with nonzero eigenvalues and then to assume a solution of the form
with nonzero eigenvalues and then to assume a solution of the form
where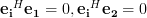 for
for 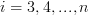 and solve for
and solve for 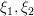 .
.
Solution: Let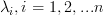 denote the eigenvalues of the matrix from which we know (by the provided hint) that only two are different from zero.
(This fact can also be directly derived by the relations (7),(9) of [2], which show that
denote the eigenvalues of the matrix from which we know (by the provided hint) that only two are different from zero.
(This fact can also be directly derived by the relations (7),(9) of [2], which show that 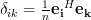 . Thus multiplying the matrix
. Thus multiplying the matrix  with
with 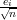 will provide the eigenvalue
will provide the eigenvalue 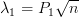 for
for 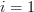 and
and 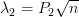 for
for 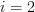 , and
, and 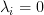 for
for 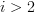 .)
The determinant of the matrix
.)
The determinant of the matrix  can be obtained by the relation
can be obtained by the relation 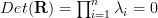 . Because the determinant is zero the matrix is singular.
Let
. Because the determinant is zero the matrix is singular.
Let 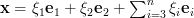 then
then
To find the solutions to the set of linear equations
we have to set (5) equal to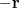 :
:
Considering the linear independence of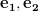 the solutions of the set of linear equations given by (7) are:
the solutions of the set of linear equations given by (7) are:
The minimum norm solution has the property that it is within the subspace spanned by the columns of the matrix [3] and thus the minimum norm solution is given by:
[3] and thus the minimum norm solution is given by: 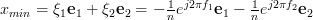 .
.
[1] Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”, Prentice Hall, ISBN: 0-13-598582-X.
[2] Chatzichrisafis: “Solution of exercise 2.8 from Kay’s Modern Spectral Estimation - Theory and Applications”, lysario.de.
[3] Chatzichrisafis: “Solution of exercise 2.4 from Kay’s Modern Spectral Estimation -Theory and Applications”, lysario.de.
 | (1) | ||
where
 is a
is a 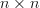 hermitian matrix given by:
hermitian matrix given by:
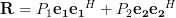 | (2) | ||
and
 is a complex
is a complex 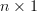 vector given by
vector given by
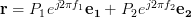 | (3) | ||
The complex vectors are defined in [1, p.22, (2.27)]. Furthermore we are asked to assumed that
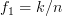 ,
, 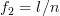 for
for 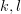 are distinct integers in the range
are distinct integers in the range ![[-n/2,n/2-1]](https://lysario.de/wp-content/cache/tex_24916734a0a5230271c84429761581eb.png) for
for  even and
even and ![[-(n-1)/2,(n-1)/2]](https://lysario.de/wp-content/cache/tex_b9ee4eee41d27a8e5eea256f738e00e2.png) for
for  odd.
odd.  is defined to be a
is defined to be a 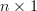 vector.
It is requested to show that
vector.
It is requested to show that  is a singular matrix (assuming
is a singular matrix (assuming 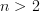 ) and that there are infinite number of solutions.
A further task is to find the general solution and also the minimum norm solution of the set of linear equations. The hint provided by the exercise is to note that
) and that there are infinite number of solutions.
A further task is to find the general solution and also the minimum norm solution of the set of linear equations. The hint provided by the exercise is to note that 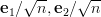 are eigenvectors of
are eigenvectors of  with nonzero eigenvalues and then to assume a solution of the form
with nonzero eigenvalues and then to assume a solution of the form
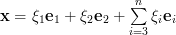 | (4) | ||
where
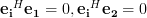 for
for 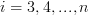 and solve for
and solve for 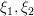 .
.
Solution: Let
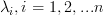 denote the eigenvalues of the matrix from which we know (by the provided hint) that only two are different from zero.
(This fact can also be directly derived by the relations (7),(9) of [2], which show that
denote the eigenvalues of the matrix from which we know (by the provided hint) that only two are different from zero.
(This fact can also be directly derived by the relations (7),(9) of [2], which show that 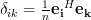 . Thus multiplying the matrix
. Thus multiplying the matrix  with
with 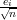 will provide the eigenvalue
will provide the eigenvalue 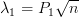 for
for 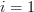 and
and 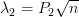 for
for 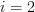 , and
, and 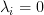 for
for 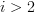 .)
The determinant of the matrix
.)
The determinant of the matrix  can be obtained by the relation
can be obtained by the relation 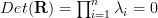 . Because the determinant is zero the matrix is singular.
Let
. Because the determinant is zero the matrix is singular.
Let 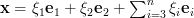 then
then
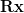 |  | 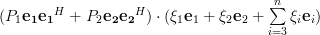 | |
 | 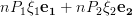 | (5) |
To find the solutions to the set of linear equations
 | (6) | ||
we have to set (5) equal to
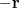 :
:
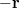 |  | 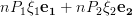 | |
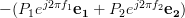 |  | 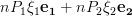 |
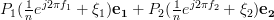 |  | 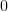 | (7) |
Considering the linear independence of
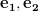 the solutions of the set of linear equations given by (7) are:
the solutions of the set of linear equations given by (7) are:
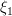 |  | 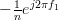 | |
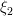 |  | 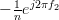 | |
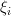 |  | 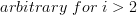 |
The minimum norm solution has the property that it is within the subspace spanned by the columns of the matrix
 [3] and thus the minimum norm solution is given by:
[3] and thus the minimum norm solution is given by: 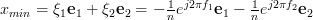 .
. [1] Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”, Prentice Hall, ISBN: 0-13-598582-X.
[2] Chatzichrisafis: “Solution of exercise 2.8 from Kay’s Modern Spectral Estimation - Theory and Applications”, lysario.de.
[3] Chatzichrisafis: “Solution of exercise 2.4 from Kay’s Modern Spectral Estimation -Theory and Applications”, lysario.de.
Leave a reply