Lysario – by Panagiotis Chatzichrisafis
"ούτω γάρ ειδέναι το σύνθετον υπολαμβάνομεν, όταν ειδώμεν εκ τίνων και πόσων εστίν …"
Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”,p. 61 exercise 3.6
Author: Panagiotis19 Apr
In [1, p. 61 exercise 3.6] we are asked to assume that the variance is to be estimated as well as the mean for the conditions of [1, p. 60 exercise 3.4] (see also [2, solution of exercise 3.4]) . We are asked to prove for the vector parameter ![\mathbf{\theta}=\left[\mu_x \; \sigma^2_x\right]^T](https://lysario.de/wp-content/cache/tex_b1d973967798bb8525bff936468f9211.png) , that the Fisher information matrix is
, that the Fisher information matrix is
Furthermore we are asked to find the CR bound and to determine if the sample mean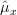 is efficient.
If additionaly the variance is to be estimated as
is efficient.
If additionaly the variance is to be estimated as
then we are asked to determine if this estimator is unbiased and efficient. Hint: We are instructed to use the result that
Solution: We have already obtained the joint pdf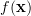 of the
of the 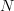 independent samples with normal distribution
independent samples with normal distribution 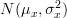 and the natural logarithm of the joint pdf is given by from [3, relation (3) ]:
and the natural logarithm of the joint pdf is given by from [3, relation (3) ]:
From this relation we can find the gradient in respect to the vector parameter:
Thus Fisher’s information matrix is given by [1, p. 47, (3.22) ]:
Considering that the samples![x[i] \;, i=0,..,N](https://lysario.de/wp-content/cache/tex_47214f3be4a9f9fabf23ed367fe4f59e.png) are independent we obtain the individual elements of the matrix
are independent we obtain the individual elements of the matrix 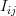 are given by:
are given by:
We note that![h(x[i])=\left(\frac{x[i]-\mu_x}{\sigma^{2}_x} \right)^{3}](https://lysario.de/wp-content/cache/tex_c6732a1b8dbe5a4501adfb197b65a1f3.png) is an odd function about
is an odd function about 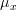 (that is
(that is 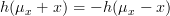 ) while the gaussian distribution is an even function about
) while the gaussian distribution is an even function about 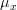 . Thus the mean of this function -the integral which is symmetric about
. Thus the mean of this function -the integral which is symmetric about 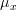 and extends from
and extends from 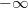 to
to 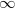 will be equal to zero. This fact can be shown by the following approach:
will be equal to zero. This fact can be shown by the following approach:
Let![u=\left(x[i]-\mu_{x}\right)](https://lysario.de/wp-content/cache/tex_ba7b6d07b92b8d66bab0265749653ea1.png) in the last formula
in the last formula
If we set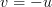 in the second integral, we obtain the following formulas:
in the second integral, we obtain the following formulas:
Using [2] in conjunction with [3] we obtain
Finally it remains to obtain the value for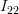 :
:
We note that![v_{i}=\frac{x[i]-\mu_x}{\sigma_x}](https://lysario.de/wp-content/cache/tex_ffdcad199afcc8629b93660aeb6dafe4.png) in (5) is a normalized random gaussian variable and that the squared sum of such variables
in (5) is a normalized random gaussian variable and that the squared sum of such variables
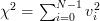 has a chi-square distribution [4, p. 682] with N degrees of freedom with mean
has a chi-square distribution [4, p. 682] with N degrees of freedom with mean 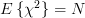 and variance equal to
and variance equal to
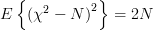 . Thus
. Thus
From (1), (4) and (6) we obtain finally that Fisher’s information matrix is equal to:
We have shown in [2, solution of exercise 3.4] that the mean and the variance [2, solution of exercise 3.4, relation (5) ] of the estimator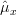 are given by:
are given by:
The mean and the variance of the estimator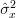 are given by (always considering the independence of the random variables
are given by (always considering the independence of the random variables ![x[n], x[k]](https://lysario.de/wp-content/cache/tex_2b0db6c4a3986293f7b951e7c4a9de00.png) for
for 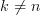 ):
):
From the previous relation we obtain finally:
Considering that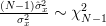 we can also obtain the variance of the estimator
we can also obtain the variance of the estimator 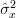 :
:
Because the Cramer Rao bound for the estimator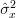 is given by the inverse of the diagonal element of Fisher’s information matrix (6)
is given by the inverse of the diagonal element of Fisher’s information matrix (6) 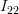 we obtain using (9) :
we obtain using (9) :
thus the estimator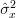 is unbiased because of (8) but not efficient because it doesn’t attain the Cramer – Rao bound given by (10).
QED.
is unbiased because of (8) but not efficient because it doesn’t attain the Cramer – Rao bound given by (10).
QED.
[1] Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”, Prentice Hall, ISBN: 0-13-598582-X.
[2] Chatzichrisafis: “Solution of exercise 3.4 from Kay’s Modern Spectral Estimation - Theory and Applications”.
[3] Chatzichrisafis: “Solution of exercise 3.5 from Kay’s Modern Spectral Estimation - Theory and Applications”.
[4] Granino A. Korn and Theresa M. Korn: “Mathematical Handbook for Scientists and Engineers”, Dover, ISBN: 978-0-486-41147-7.
![\mathbf{\theta}=\left[\mu_x \; \sigma^2_x\right]^T](https://lysario.de/wp-content/cache/tex_b1d973967798bb8525bff936468f9211.png) , that the Fisher information matrix is
, that the Fisher information matrix is
![\mathbf{I}_{\theta}=\left[\begin{array}{cc} \frac{N}{\sigma^2_x} & 0 \\ 0 & \frac{N}{2\sigma^4_x} \end{array}\right]](https://lysario.de/wp-content/cache/tex_42789b24f24a6a32db03314ccac291c8.png) | |||
Furthermore we are asked to find the CR bound and to determine if the sample mean
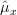 is efficient.
If additionaly the variance is to be estimated as
is efficient.
If additionaly the variance is to be estimated as
![\hat{\sigma}^2_x=\frac{1}{N-1}\sum\limits_{n=0}^{N-1}(x[n]-\hat{\mu}_x)^2](https://lysario.de/wp-content/cache/tex_13d6ef5f9b8f0b1d9832efd9b58af88b.png) | |||
then we are asked to determine if this estimator is unbiased and efficient. Hint: We are instructed to use the result that
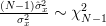 | |||
Solution: We have already obtained the joint pdf
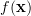 of the
of the 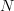 independent samples with normal distribution
independent samples with normal distribution 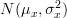 and the natural logarithm of the joint pdf is given by from [3, relation (3) ]:
and the natural logarithm of the joint pdf is given by from [3, relation (3) ]:
 |  | ![-\ln(\sqrt{2\pi}\sigma_x)N-\frac{1}{2}\sum\limits_{i=0}^{N-1}\left(\frac{x[i]-\mu_x}{\sigma_x}\right)^2](https://lysario.de/wp-content/cache/tex_d70aee1bec5c1013d3e79f140db20654.png) | |
 | ![-\frac{N}{2}\ln(2\pi \sigma^{2}_x)-\frac{1}{2}\sum\limits_{i=0}^{N-1}\left(\frac{x[i]-\mu_x}{\sigma_x}\right)^2](https://lysario.de/wp-content/cache/tex_b0debdaa5cd11556e9c4db5a4490619b.png) |
From this relation we can find the gradient in respect to the vector parameter:
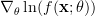 |  | ![\left[ \begin{array}{cc} \frac{\partial \ln(f(\mathbf{x};\theta))}{\partial \mu_{x}} & \frac{\partial \ln(f(\mathbf{x};\theta))}{\partial \sigma^{2}_{x}} \end{array} \right]^{T}](https://lysario.de/wp-content/cache/tex_8f8126a7cecf6f0790fec3dc60b117dc.png) | |
 | ![\left[ \begin{array}{cc} \sum_{i=0}^{N-1}\left(\frac{x[i]-\mu_x}{\sigma^{2}_x}\right) & -\frac{N}{2\sigma_{x}^{2}}+\frac{1}{2} \sum_{i=0}^{N-1}\frac{\left(x[i]-\mu_x\right)^2}{\sigma^{4}_x}\end{array} \right]^{T}](https://lysario.de/wp-content/cache/tex_316fe977824c4e41b259a44eb32121e0.png) |
Thus Fisher’s information matrix is given by [1, p. 47, (3.22) ]:
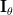 |  | 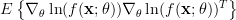 |
Considering that the samples
![x[i] \;, i=0,..,N](https://lysario.de/wp-content/cache/tex_47214f3be4a9f9fabf23ed367fe4f59e.png) are independent we obtain the individual elements of the matrix
are independent we obtain the individual elements of the matrix 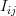 are given by:
are given by:
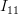 |  | ![E\left\{ \left(\sum\limits_{i=0}^{N-1}\left(\frac{x[i]-\mu_x}{\sigma^{2}_x}\right) \right)^{2} \right\}](https://lysario.de/wp-content/cache/tex_792f46c5e2010423fd7d5530c704ebce.png) | |
 | ![E\left\{ \sum\limits_{i=0}^{N-1}\frac{\left(x[i]-\mu_x\right)^{2}}{\sigma^{4}_x} +\sum\limits_{i=0}^{N-1}\sum\limits_{j=0,j\neq i}^{N-1}\frac{\left(x[i]-\mu_x\right)\left(x[j]-\mu_x\right)}{\sigma^{4}_x} \right\}](https://lysario.de/wp-content/cache/tex_753e53f6b6a2aafe935f391d3f0e3fab.png) | ||
 | ![\sum\limits_{i=0}^{N-1}\frac{E\left\{ \left(x[i]-\mu_x\right)^{2}\right\}}{\sigma^{4}_x}](https://lysario.de/wp-content/cache/tex_8bf310ccf6cecd51efd069b42ed7d317.png) | ||
 | ![+\sum\limits_{i=0}^{N-1}\sum\limits_{j=0,j\neq i}^{N-1}\frac{E\left\{\left(x[i]-\mu_x\right)\right\}E\left\{\left(x[j]-\mu_x\right)\right\}}{\sigma^{4}_x}](https://lysario.de/wp-content/cache/tex_928ebf2a7a124a71aec67749671b167d.png) | ||
 | 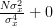 | ||
 | 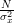 | (1) | |
 |  | ![E\left\{ \left(\sum\limits_{i=0}^{N-1}\left(\frac{x[i]-\mu_x}{\sigma^{2}_x}\right) \right) \left(-\frac{N}{2\sigma_{x}^{2}}+\frac{1}{2} \sum\limits_{i=0}^{N-1}\frac{\left(x[i]-\mu_x\right)^2}{\sigma^{4}_x}\right) \right\}](https://lysario.de/wp-content/cache/tex_c04b3f411453cd48319328d58820ebe6.png) | |
 | ![E\left\{ -\frac{N}{2 \sigma_{x}^{2} } \sum\limits_{i=0}^{N-1} \left(\frac{x[i]-\mu_x}{\sigma^{2}_x}\right)\right\}](https://lysario.de/wp-content/cache/tex_73a6d5b8ec75fc97dda66f145453710b.png) | ||
 | ![+E\left\{ \left(\sum\limits_{i=0}^{N-1}\frac{x[i]-\mu_x}{\sigma^{2}_x} \right) \left(\frac{1}{2}\sum\limits_{i=0}^{N-1}\frac{\left( x[i]-\mu_x \right)^2}{\sigma^{4}_x}\right) \right\}](https://lysario.de/wp-content/cache/tex_aba4104a454ffb06677a3ae02775d202.png) | ||
 | ![-\frac{N}{2 \sigma_{x}^{2} } \sum\limits_{i=0}^{N-1} \left(\frac{E\left\{x[i]\right\}-\mu_x}{\sigma^{2}_x}\right)
+\frac{1}{2}E\left\{ \sum\limits_{i=0}^{N-1}\left(\frac{x[i]-\mu_x}{\sigma^{2}_x} \right)^{3}\right\}](https://lysario.de/wp-content/cache/tex_010392e342611bc4911507b6a786915d.png) | ||
 | ![+ \frac{1}{2}E\left\{\sum\limits_{i=0}^{N-1} \sum\limits_{j=0,j\neq i}^{N-1}\frac{\left(x[j]-\mu_x\right)\left( x[i]-\mu_x \right)^2}{\sigma^{6}_x} \right\}](https://lysario.de/wp-content/cache/tex_e3f4c83432f37c3a544bafd8844c5472.png) | ||
 | ![0+\frac{1}{2} E\left\{ \sum\limits_{i=0}^{N-1}\left(\frac{x[i]-\mu_x}{\sigma^{2}_x} \right)^{3}\right\}](https://lysario.de/wp-content/cache/tex_78286af501c19fc5483328ddaec0be5b.png) | ||
 | ![+\frac{1}{2}\sum\limits_{i=0}^{N-1} \sum\limits_{j=0,j\neq i}^{N-1}\frac{ E\left\{\left(x[j]-\mu_x\right)\left( x[i]-\mu_x \right)^2\right\}}{\sigma^{6}_x}](https://lysario.de/wp-content/cache/tex_9d8ab121240ac809606624347a76410c.png) | ||
 | ![\frac{1}{2}E\left\{ \sum\limits_{i=0}^{N-1}\left(\frac{x[i]-\mu_x}{\sigma^{2}_x} \right)^{3}\right\}](https://lysario.de/wp-content/cache/tex_7ebdfee13e758847e5f688c756467083.png) | ||
 | ![+\frac{1}{2}\sum\limits_{i=0}^{N-1} \sum\limits_{j=0,j\neq i}^{N-1}\frac{ E\left\{\left(x[j]-\mu_x\right)\right\}E\left\{\left( x[i]-\mu_x \right)^2\right\}}{\sigma^{6}_x}](https://lysario.de/wp-content/cache/tex_12f77a724849dcd55fabe1b005221eed.png) | ||
 | ![\frac{1}{2} E\left\{ \sum\limits_{i=0}^{N-1}\left(\frac{x[i]-\mu_x}{\sigma^{2}_x} \right)^{3}\right\} +0](https://lysario.de/wp-content/cache/tex_6ef454ab2a25b36d61fc59e8a5cd4465.png) | ||
 | ![\frac{1}{2} \sum\limits_{i=0}^{N-1}E\left\{\left(\frac{x[i]-\mu_x}{\sigma^{2}_x} \right)^{3} \right\}](https://lysario.de/wp-content/cache/tex_bed7fc9813146d9c54133fce464e5383.png) | (2) |
We note that
![h(x[i])=\left(\frac{x[i]-\mu_x}{\sigma^{2}_x} \right)^{3}](https://lysario.de/wp-content/cache/tex_c6732a1b8dbe5a4501adfb197b65a1f3.png) is an odd function about
is an odd function about 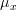 (that is
(that is 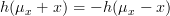 ) while the gaussian distribution is an even function about
) while the gaussian distribution is an even function about 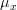 . Thus the mean of this function -the integral which is symmetric about
. Thus the mean of this function -the integral which is symmetric about 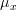 and extends from
and extends from 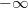 to
to 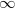 will be equal to zero. This fact can be shown by the following approach:
will be equal to zero. This fact can be shown by the following approach:
![E\left\{\left(\frac{x[i]-\mu_x}{\sigma^{2}_x} \right)^{3} \right\}](https://lysario.de/wp-content/cache/tex_afca19da303893e83b6fcffb7182e25e.png) |  | ![\frac{1}{\sqrt{2\pi}\sigma_{x}}\int_{-\infty}^{+\infty}\left(\frac{x[i]-\mu_x}{\sigma^{2}_x} \right)^{3}e^{-\left(\frac{x[i]-\mu_{x}}{\sigma_{x}}\right)^{2}} dx](https://lysario.de/wp-content/cache/tex_3c9f7e91efb09b74d9bdd80c47965fac.png) | |
 | ![\frac{1}{\sqrt{2\pi}\sigma_{x}}\int_{-\infty}^{\mu_{x}}\left(\frac{x[i]-\mu_x}{\sigma^{2}_x} \right)^{3}e^{-\left(\frac{x[i]-\mu_{x}}{\sigma_{x}}\right)^{2}} dx](https://lysario.de/wp-content/cache/tex_4e9064648161579be317450b6cddf0ae.png) | ||
 | ![+\frac{1}{\sqrt{2\pi}\sigma_{x}}\int_{\mu_{x}}^{+\infty}\left(\frac{x[i]-\mu_x}{\sigma^{2}_x} \right)^{3}e^{-\left(\frac{x[i]-\mu_{x}}{\sigma_{x}}\right)^{2}} dx](https://lysario.de/wp-content/cache/tex_6263ae551b2578a05f7f5b86c0a404af.png) |
Let
![u=\left(x[i]-\mu_{x}\right)](https://lysario.de/wp-content/cache/tex_ba7b6d07b92b8d66bab0265749653ea1.png) in the last formula
in the last formula
![E\left\{\left(\frac{x[i]-\mu_x}{\sigma^{2}_x} \right)^{3} \right\}](https://lysario.de/wp-content/cache/tex_afca19da303893e83b6fcffb7182e25e.png) |  | 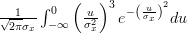 | |
 | 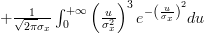 | ||
 | 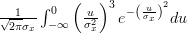 | ||
 | 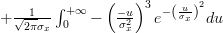 | ||
 | 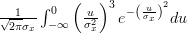 | ||
 | 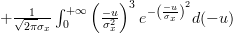 |
If we set
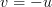 in the second integral, we obtain the following formulas:
in the second integral, we obtain the following formulas:
![E\left\{\left(\frac{x[i]-\mu_x}{\sigma^{2}_x} \right)^{3} \right\}](https://lysario.de/wp-content/cache/tex_afca19da303893e83b6fcffb7182e25e.png) |  | 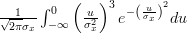 | |
 | 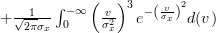 | ||
 |  | ||
 | 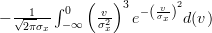 | ||
![E\left\{\left(\frac{x[i]-\mu_x}{\sigma^{2}_x} \right)^{3} \right\}](https://lysario.de/wp-content/cache/tex_afca19da303893e83b6fcffb7182e25e.png) |  | 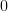 | (3) |
Using [2] in conjunction with [3] we obtain
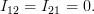 | (4) | ||
Finally it remains to obtain the value for
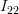 :
:
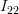 |  | ![E\left\{\left( -\frac{N}{2\sigma_{x}^{2}}+\frac{1}{2} \sum\limits_{i=0}^{N-1}\frac{\left(x[i]-\mu_x\right)^2}{\sigma^{4}_x}\right)^{2}\right\}](https://lysario.de/wp-content/cache/tex_ebff0c112204a26381e1b6d2e195131d.png) | |
 | ![\frac{1}{4\sigma_{x}^{4}} E\left\{\left( \sum\limits_{i=0}^{N-1}\left(\frac{x[i]-\mu_x}{\sigma_x}\right)^{2} -N\right)^{2}\right\}](https://lysario.de/wp-content/cache/tex_1407c36863a9d98363e7b66da305ee07.png) | (5) |
We note that
![v_{i}=\frac{x[i]-\mu_x}{\sigma_x}](https://lysario.de/wp-content/cache/tex_ffdcad199afcc8629b93660aeb6dafe4.png) in (5) is a normalized random gaussian variable and that the squared sum of such variables
in (5) is a normalized random gaussian variable and that the squared sum of such variables
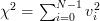 has a chi-square distribution [4, p. 682] with N degrees of freedom with mean
has a chi-square distribution [4, p. 682] with N degrees of freedom with mean 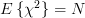 and variance equal to
and variance equal to
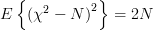 . Thus
. Thus
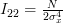 | (6) | ||
From (1), (4) and (6) we obtain finally that Fisher’s information matrix is equal to:
![\mathbf{I}_{\theta}=\left[ \begin{array}{cc} \frac{N}{\sigma_{x}^{2}} & 0 \\ 0 &\frac{N}{2\sigma_{x}^{4}} \end{array} \right].](https://lysario.de/wp-content/cache/tex_3b0698479493ccbebcb94f2b171905d4.png) | (7) | ||
We have shown in [2, solution of exercise 3.4] that the mean and the variance [2, solution of exercise 3.4, relation (5) ] of the estimator
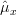 are given by:
are given by:
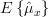 |  | 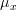 | |
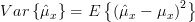 |  | 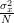 |
The mean and the variance of the estimator
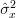 are given by (always considering the independence of the random variables
are given by (always considering the independence of the random variables ![x[n], x[k]](https://lysario.de/wp-content/cache/tex_2b0db6c4a3986293f7b951e7c4a9de00.png) for
for 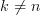 ):
):
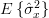 |  | ![\frac{1}{N-1}\sum\limits_{n=0}^{N-1}E\left\{(x[n]-\hat{\mu}_{x})^{2}\right\}](https://lysario.de/wp-content/cache/tex_cb3bcfe8a78cbcfe97e2e5bea783b5f6.png) | |
 | ![\frac{1}{N-1}\sum\limits_{n=0}^{N-1}E\left\{((x[n]-\mu_{x})- (\hat{\mu}_{x}-\mu_{x}))^{2}\right\}](https://lysario.de/wp-content/cache/tex_231dd0454e424691213f11b75cbc92ce.png) | ||
 | ![\frac{1}{N-1}\sum\limits_{n=0}^{N-1}E\left\{(x[n]-\mu_{x})^{2}\right\}+\frac{1}{N-1}\sum\limits_{n=0}^{N-1} E\left\{(\hat{\mu}_{x}-\mu_{x})^{2}\right\}](https://lysario.de/wp-content/cache/tex_3d00a79760b79a0e3848b68664988764.png) | ||
 | ![- \frac{2}{N-1}\sum\limits_{n=0}^{N-1}E\left\{(x[n]-\mu_{x})(\hat{\mu}_{x}-\mu_{x})\right\}](https://lysario.de/wp-content/cache/tex_d8b2279930f39c7fc227f711592f0d18.png) | ||
 | ![\frac{N\sigma^{2}_{x}}{N-1} + \frac{\sigma^{2}_{x}}{N-1} - \frac{2}{N-1}\sum\limits_{n=0}^{N-1}E\left\{(x[n]-\mu_{x})(\hat{\mu}_{x}-\mu_{x})\right\}](https://lysario.de/wp-content/cache/tex_471dd6e5191e8180c8363b4f2ca415cc.png) | ||
 | ![\frac{(N+1)\sigma^{2}_{x}}{N-1} - \frac{2}{N-1}\sum\limits_{n=0}^{N-1}E\left\{(x[n]-\mu_{x})(\hat{\mu}_{x}-\mu_{x})\right\}](https://lysario.de/wp-content/cache/tex_b010f17a02ef30803066e9744eff0902.png) | ||
 | ![\frac{(N+1)\sigma^{2}_{x}}{N-1} - \frac{2}{N-1}\sum\limits_{n=0}^{N-1}E\left\{(x[n]-\mu_{x})(\frac{1}{N}\sum\limits_{i=0}^{N-1}x[i]-\mu_{x})\right\}](https://lysario.de/wp-content/cache/tex_799df226eef47a5c70ad69bf0a168ee4.png) | ||
 | ![\frac{(N+1)\sigma^{2}_{x}}{N-1} - \frac{2}{N-1}\sum\limits_{n=0}^{N-1}E\left\{\frac{1}{N}(x[n]-\mu_{x})(\sum\limits_{i=0}^{N-1}(x[i]-\mu_{x}))\right\}](https://lysario.de/wp-content/cache/tex_c74f3bbf988a63c99ee0571016b2d8b7.png) | ||
 | 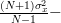 | ||
 | ![\frac{2}{N-1}\sum\limits_{n=0}^{N-1}\frac{1}{N}\Bigg( E\left\{(x[n]-\mu_{x})^{2}\right\}](https://lysario.de/wp-content/cache/tex_22c74ad89e814b2d8938483b6629a349.png) | ||
 | ![\left. +\sum\limits_{i=0,i\neq n}^{N-1}E\left\{(x[n]-\mu_{x})(x[i]-\mu_{x})\right\} \right)](https://lysario.de/wp-content/cache/tex_f09a7fbef01d723cdd397005eb47e54d.png) | ||
 | 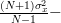 | ||
 | 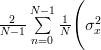 | ||
 | ![+\sum\limits_{i=0,i\neq n}^{N-1}E\left\{(x[n]-\mu_{x})\right\}E\left\{(x[i]-\mu_{x})\right\} \Bigg)](https://lysario.de/wp-content/cache/tex_76d0bb291df21da89c9f62716bdb789e.png) | ||
 | 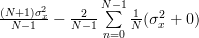 | ||
 | 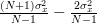 |
From the previous relation we obtain finally:
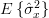 |  |  | (8) |
Considering that
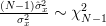 we can also obtain the variance of the estimator
we can also obtain the variance of the estimator 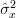 :
:
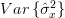 |  | 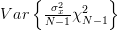 | |
 | 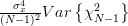 | ||
 | 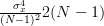 | ||
 | 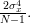 | (9) |
Because the Cramer Rao bound for the estimator
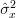 is given by the inverse of the diagonal element of Fisher’s information matrix (6)
is given by the inverse of the diagonal element of Fisher’s information matrix (6) 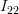 we obtain using (9) :
we obtain using (9) :
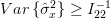 | |||
 | (10) | ||
thus the estimator
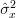 is unbiased because of (8) but not efficient because it doesn’t attain the Cramer – Rao bound given by (10).
QED.
is unbiased because of (8) but not efficient because it doesn’t attain the Cramer – Rao bound given by (10).
QED.
[1] Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”, Prentice Hall, ISBN: 0-13-598582-X.
[2] Chatzichrisafis: “Solution of exercise 3.4 from Kay’s Modern Spectral Estimation - Theory and Applications”.
[3] Chatzichrisafis: “Solution of exercise 3.5 from Kay’s Modern Spectral Estimation - Theory and Applications”.
[4] Granino A. Korn and Theresa M. Korn: “Mathematical Handbook for Scientists and Engineers”, Dover, ISBN: 978-0-486-41147-7.
One Response for "Steven M. Kay: “Modern Spectral Estimation – Theory and Applications”,p. 61 exercise 3.6"
[...] The mean of the maximum likelihood estimator of the variance can be easily obtained using [4, relation (8)] and noting that the maximum likelihood estimator of the variance is times the variance estimator [...]
Leave a reply